|
|
LEHRVERANSTALTUNGEN
HS23 - Grundstudium: LINEARE ALGEBRA I
In dieser Lehrveranstaltung und ihrer Fortsetzung im Frühjahrsemester 2020
behandeln wir die Grundlagen der linearen Algebra, welche in allen weiterführenden
Vorlesungen und Seminaren in Mathematik und Physik vorausgesetzt werden.
Behandelt werden in diesem Semester Gruppen, Vektorräume, lineare
Gleichungssysteme, Matrizen und lineare Abbildungen.
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Marta Dujella (EN), Mani Esna Ashari (EN), Alexander Heinimann (DE), Alex Merstetter (DE), Anne Schnattinger (DE) |
|
Vorlesung: | Montag 10.15 -12.00 Uhr, Kollegienhaus, Hörsaal 115
Dienstag 8.15 -10.00 Uhr, Kollegienhaus, Hörsaal 116 |
|
Übungen: |
|
11038-01 (EN) | Mittwoch
10h15-12h | Kollegienhaus,
Hörsaal 106 | Mani
Esna Ashari
|
|
11038-02 (DE) | Donnerstag
10h15-12h | Spiegelgasse 1,
Seminarraum 00.003 | Anne
Schnattinger
|
|
11038-03 (EN) | Donnerstag
10h15-12h | Spiegelgasse 5,
Seminarraum 05.001 | Marta
Dujella
|
|
11038-04 (DE) | Freitag
10h15-12h | Physik,
Seminarzimmer 4.1 | Alex
Merstetter
|
|
11038-05 (DE) | Mittwoch
10h15-12h | Chemie, Physikalische,
Kleiner Hörsaal PC 4.04 | Alexander
Heinimann
|
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein.
Jede Woche gibt es ein Blatt:
|
Standardprogramm: |
Die Aufgaben vom Standardprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur nach dem Semester bestehen,
und zwar am Montag, den 8. Januar 2024, 09.30 - 10.30 Uhr (Kollegienhaus, Hörsaal 115).
Wiederholungsklausur: 22. Januar 2024, 09.30 - 10.30 Uhr (Kollegienhaus, Hörsaal 115).
|
Ergänzungsprogramm:
|
Die Aufgaben vom Ergänzungsprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Montag, den 8. Januar 20224, 10.45 -11.45 Uhr (Kollegienhaus, Hörsaal 115).
Wiederholungsklausur: 22. Januar 2024, 10.45 -11.45 Uhr (Kollegienhaus, Hörsaal 115).
|
Auszug aus der Literatur:
|
G. Fischer | Lineare Algebra. | Vieweg Verlag.
|
HS22 MASTERVERTIEFUNGSMODUL:
Algebraische Geometrie I
Algebraische Geometrie studiert geometrische Objekte, die als Lösungen von Polynomgleichungen definiert sind. Viele bekannte geometrische Objekte können als Lösungsmenge von geeigneten Polynomgleichungen beschrieben werden: Kreise, Kugeln, Hyperbeln,...
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistentin: | Anna Bot
|
|
Vorlesung: |
Dienstag 14.15 -16.00 Uhr
Mittwoch 10.15 -12.00 Uhr
|
|
Übungen: | Donnerstag 14.15 -16.00 Uhr
|
|
|
|
Zur Erlangung der Kreditpunkte müssen die Übungen bearbeitet sein, und die Klausur bestanden sein.
Auszug aus der Literatur:
|
M. Reid | Undergraduate algebraic geometry. | London Mathematical Society Student Texts.
| |
I. R. Shafarevich | Basic algebraic geometry. 1.+ 2. | Springer.
| |
K. Hulek | Elementare Algebraische Geometrie. | vieweg studium, Aufbaukurs Mathematik.
|
|
W. Fulton | Algebraic curves. | Web page of W. Fulton.
|
|
G. Fischer | Ebene algebraische Kurven. | vieweg studium, Aufbaukurs Mathematik.
| |
R. Hartshorne | Algebraic geometry. | Springer.
| |
M. Brodman | Algebraische Geometrie - Eine Einführung. | Basler Lehrbücher - Birkhauser
|
FS22 - Grundstudium: LINEARE ALGEBRA II
In dieser Lehrveranstaltung, wie in Lineare Algebra I behandeln wir die Grundlagen der linearen Algebra, welche in allen weiterführenden Vorlesungen und Seminaren in Mathematik und Physik vorausgesetzt werden.
Behandelt werden in diesem Semester Determinante, Konjugationsklassen, Normalformen, Eigenvektoren, Diagonalisierbarkeit, Drehungen und Spiegelungen, Bilinearformen, Dualen...
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Raphael Erb, Mani Esna-Ashari, Pascal Fong, Irène Meunier |
|
Vorlesung: | Montag 10.15 -12.00 Uhr, Kollegienhaus, Hörsaal 116 (Petersplatz 1, Basel)
Dienstag 8.15 -10.00 Uhr, Kollegienhaus, Hörsaal 116 (Petersplatz 1, Basel) |
|
Übungen: |
|
11038-01 | Mittwoch
10h15-12h | Kollegienhaus,
Hörsaal 119 | Pascal
Fong (DE)
|
|
11038-02 | Donnerstag
10h15-12h | Bernoullistrasse 30/32,
kleiner Hörsaal 120 | Irène
Meunier (EN)
|
|
11038-03 | Donnerstag
10h15-12h | Kollegienhaus,
Seminarraum 104 | Mani
Esna-Ashari (EN)
|
|
11038-04 | Freitag
10h15-12h | Deutsches Seminar (Nadelweg 4)
Seminarraum 4 | Raphael
Erb (DE)
|
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein.
Jede Woche gibt es ein Blatt (auf Adam).
|
Standardprogramm: |
Die Aufgaben vom Standardprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Dienstag, den 7. Juni 2022, 10.00 - 10.55 Uhr.
Wiederholungsklausur: 21. Juni 2022, 10.00-10.55 Uhr-
|
Ergänzungsprogramm:
|
Die Aufgaben vom Ergänzungsprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Dienstag, den 7. Juni 2022, 11.05 -12.05 Uhr.
Wiederholungsklausur: 21. Juni 2022, 11.05-12.05 Uhr
|
Auszug aus der Literatur:
|
G. Fischer | Lineare Algebra. | Vieweg Verlag.
|
FS22 - SEMINAR: Transformationsgruppen Geometrie
Das Seminar studiert Operationen von Gruppen auf geometrischen Objekten. Wir folgen zwei Bücher, nämlich
(A) M. A. Armstrong - Groups and symmetry- 1988
(M) John Meier, groups, graphs and trees - 2012
und werden auch Webseite von Keith Conrad und David Newcomb folgen (vgl unten).
|
Dozent: | Jérémy Blanc |
|
Assistent: | Sokratis Zikas |
|
Zeit und Ort: | Montag 16.15 -18.00 Uhr, Spiegelgasse 1, Seminarraum 00.003 (EG) |
|
Programm: |
|
21.02.2022: | Vorbesprechung und Verteilung der Vorträge |
|
14.03.2022: | Yannick Caspar | Diedral groups | Chapter 4 of (A) |
|
21.03.2022: | Ricardo Grieco | Platonic solids | Webpage of David Newcomb |
|
28.03.2022: | Denis Rakazovi | Finite rotation groups | Chapter 19 of (A) |
|
04.04.2022: | Yari Volpe | The Euclidean group | Chapter 24 of (A) |
|
11.04.2022: | Federico Frattini | Simplicity of PSLn(K) | Webpage of Keith Conrad |
|
02.05.2022: | Elias Kurz | Symmetry groups of graphs | pages 6-15 of (M) |
|
09.05.2022: | Lukas Hilgert | Cayley graphs | pages 18-19 & 21-27 of (M) |
|
16.05.2022: | Baumslag-Solitar groups | Katarina Trailovic | pages 100-104 of (M) |
|
23.05.2022: | Words and Dehn's word problem | Travis Rivera | pages 105-115 of (M) |
|
HS21 - Aufbaustudium: ALGEBRA
Die Algebra untersucht allgemeine Strukturen, sie bildet einen fundamentalen Block für alle anderen Gebiete der Mathematik.
In dieser Vorlesung werden wir Gruppe und Ringe studieren. In dieser Hauptvorlesung werden die Grundlagen der Algebra behandelt. Sie findet im FS2022 eine Fortsetzung in Algebra II.
Inhalt:
1) Gruppentheorie: Grundlagen, Quotiente und Produkte von Gruppen, Gruppenoperationen, Sylow-Sätze, Beispiele
2) Ringe: Grundlagen, Ideale, Primideale, maximale Ideale, Quotienten, Hauptidealringe, faktorielle Ringe, Lokalisierung
3) Modultheorie mit Schwerpunkt Moduln über einem Hauptidealring.
4) Einführung in die Körpertheorie: Körpererweiterungen, Zerfällungskörper, Satz des primitiven Elements
*** Alles findet im Präsenz statt (mit Live-Zoom für die Vorlesung, ohne Aufnahme)***
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Marta Dujella, Pascal Fong, Irène Meunier
|
|
Vorlesung: | Dienstag 14.15 -16.00 Uhr (Biozentrum Neubau, U1.141)
Mittwoch 8.15 -10.00 Uhr (Kollegienhaus, 118)
|
|
Klausur: |
22 Dezember 2021, 08h15 im Kollegienhaus, 118.
|
|
Mündliche Prüfung: |
31.1.2022-4.2.2022, Spiegelgasse 1-5.
|
|
Wiederholungsklausur: |
8.2.2022, 14h15-16h, Alte Uni, 101.
|
|
Übungen: |
|
Donnerstag | 14h15-16h00 | Spiegelgasse 5, Seminarraum 05.002 | Marta Dujella |
|
Freitag | 10h15-12h00 | Spiegelgasse 5, Seminarraum 05.002 | Irène Meunier |
|
Freitag | 14h15-16h00 | Spiegelgasse 1, Seminarraum 00.003 | Anna Bot |
Übungen finden Sie auf Adam.
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein.
Auszug aus der Literatur:
HS20 -FS21 MASTERVERTIEFUNGSMODUL:
Algebraische Geometrie I + II
Algebraische Geometrie studiert geometrische Objekte, die als Lösungen von Polynomgleichungen definiert sind. Viele bekannte geometrische Objekte können als Lösungsmenge von geeigneten Polynomgleichungen beschrieben werden: Kreise, Kugeln, Hyperbeln,...
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistentin: | Sokratis Zikas (HS20) -- Pascal Fong (FS21)
pascal fong fong  unibas unibas ch ch
|
|
Vorlesung: |
HS20: Die Vorlesung finden Sie online auf switch tube. Es gab dann Fragenstunden jede Woche.
FS21: Die Vorlesung war online und ist jetzt auch in Spiegelgasse 1.
Dienstag 14.15 -16.00 Uhr
Mittwoch 10.15 -12.00 Uhr
Donnerstag 14.15 -16.00 Uhr (Übungen)
|
|
Klausur: |
Mittwoch, 16 Dezember 2020, 10.15 -12.00 Uhr (Spiegelgasse 1, Seminarraum 00.003)
Dienstag, 6 Juni 2021, 14.15 -16.00 Uhr (Spiegelgasse 1, Seminarraum 00.003)
|
|
Übungen: |
Die Übungen: sind auf Adam und müssen online hochgeladet sein sein.
|
|
|
|
Zur Erlangung der Kreditpunkte müssen die Übungen bearbeitet sein, und die Klausur bestanden sein.
Auszug aus der Literatur:
|
M. Reid | Undergraduate algebraic geometry. | London Mathematical Society Student Texts.
| |
I. R. Shafarevich | Basic algebraic geometry. 1.+ 2. | Springer.
| |
K. Hulek | Elementare Algebraische Geometrie. | vieweg studium, Aufbaukurs Mathematik.
|
|
W. Fulton | Algebraic curves. | Web page of W. Fulton.
|
|
G. Fischer | Ebene algebraische Kurven. | vieweg studium, Aufbaukurs Mathematik.
| |
R. Hartshorne | Algebraic geometry. | Springer.
| |
M. Brodman | Algebraische Geometrie - Eine Einführung. | Basler Lehrbücher - Birkhauser
|
FS20 - Aufbaustudium: Gruppenkohomologie
In dieser Vorlesung werden wird Gruppen einführen, und dann Untergruppen, Homomorphismen, Faktorgruppen,... Wir werden dann die Kohomologiemengen H0(G,A) und H1(G,A) definieren, wenn G eine Gruppe ist, die auf einer anderen Gruppe A operiert. Und auch die Kohomologiegruppen Hn(G,A) für jedes n, wenn A abelsch ist.
Wir werden lernen, wie man Kohomologiemengen berechnet (mit Hilbert 90 und exakten Folgen) und Anwendungen dieser Mengen in der Gruppen-, Algebren- und Zahlentheorie studieren.
*** Jetzt findet die Vorlesung online statt (22.9 und 23.9). Jeder Montag um 16h15 gibt es ein ZOOM-Meeting. Die Uebungen sind auch durch ZOOM. Alle Informationen finden Sie auf ADAM. Wenn Sie kein Zugriff haben, fragen Sie den Dozent durch Email.***
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistent: | Sokratis Zikas |
|
Vorlesung: | Montag 16.15 -18.00 Uhr, Spiegelgasse 5, Seminarraum 05.001.
|
|
Übungen: | Donnerstag 14.15-16.00 Uhr, Spiegelgasse 1, Seminarraum 00.003. |
Auszug aus der Literatur:
|
G. Fischer | Lehrbuch der Algebra. | Springer.
|
|
S. Bosch | Algebra. | Springer.
| |
I. R. Shafarevich | Algebra I. | Springer.
| |
J.-P. Serre | Local fields. | Springer.
|
FS20 - Grundstudium: LINEARE ALGEBRA II
In dieser Lehrveranstaltung, wie in Lineare Algebra I behandeln wir die Grundlagen der linearen Algebra, welche in allen weiterführenden
Vorlesungen und Seminaren in Mathematik und Physik vorausgesetzt werden.
Behandelt werden in diesem Semester Determinante, Konjugationsklassen, Normalformen, Eigenvektoren, Diagonalisierbarkeit, Bilinearformen, Dualen...
*** Jetzt findet die Vorlesung online statt. Die Vorlesung finden Sie auf Switchtube (Videos). Fragestunden ueber die Vorlesung finden am Montag um 11h00 und am Dienstag um 9h15 auf ZOOM statt. Die Uebungen sind auch durch ZOOM, am Donnerstag 10h (Englisch) und Freitag 10h (Deutsch). Alle Informationen finden Sie auf ADAM. Wenn Sie kein Zugriff haben, fragen Sie den Dozent durch Email.***
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Pascal Fong, Myrto Mavraki, Richard Griffon, Robert Wilms |
|
Vorlesung: | Montag 10.15 -12.00 Uhr, Kollegienhaus, Hörsaal 116 (Petersplatz 1, Basel)
Dienstag 8.15 -10.00 Uhr, Kollegienhaus, Hörsaal 116 (Petersplatz 1, Basel) |
|
Übungen: |
|
11038-01 | Mittwoch
10h15-12h | Bernoullistrasse 30/32
kleiner Hörsaal 120 | Pascal
Fong
|
|
11038-02 | Donnerstag
10h15-12h | Bernoullistrasse 30/32,
kleiner Hörsaal 120 | Myrto
Mavraki
|
|
11038-03 | Donnerstag
10h15-12h | Kollegienhaus,
Seminarraum 104 | Richard
Griffon
|
|
11038-04 | Freitag
10h15-12h | Kollegienhaus,
Seminarraum 104 | Robert
Wilms
|
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein.
Jede Woche gibt es ein Blatt:
|
Standardprogramm: |
Die Aufgaben vom Standardprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Montag, den 25. Mai 2020, 10.15 - 11.15 Uhr (Physikgebäude vgl Email).
Wiederholungsklausur: 22. Juni 2020 auf Anmeldung durch Adam (geschlossen), Informationen durch Email
|
Ergänzungsprogramm:
|
Die Aufgaben vom Ergänzungsprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Montag, den 25. Mai 2020, 11.30 -12.30 Uhr (Physikgebäude vgl Email).
Wiederholungsklausur: 22. Juni 2020 auf Anmeldung durch Adam (geschlossen), Informationen durch Email
|
Auszug aus der Literatur:
|
G. Fischer | Lineare Algebra. | Vieweg Verlag.
|
HS19 - Grundstudium: LINEARE ALGEBRA I
In dieser Lehrveranstaltung und ihrer Fortsetzung im Frühjahrsemester 2020
behandeln wir die Grundlagen der linearen Algebra, welche in allen weiterführenden
Vorlesungen und Seminaren in Mathematik und Physik vorausgesetzt werden.
Behandelt werden in diesem Semester Gruppen, Vektorräume, lineare
Gleichungssysteme, Matrizen und lineare Abbildungen.
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Gabriel Dill , Marta Dujella , Christoph Puetz, Sokratis Zikas |
|
Vorlesung: | Montag 10.15 -12.00 Uhr, Alte Universität, Hörsaal 101 (Rheinsprung 9, Basel)
Dienstag 8.15 -10.00 Uhr, Alte Universität, Hörsaal 101 (Rheinsprung 9, Basel) |
|
Übungen: |
|
11038-01 | Mittwoch
10h15-12h | Kollegienhaus,
Hörsaal 114 | Sokratis
Zikas
|
|
11038-02 | Donnerstag
10h15-12h | Bernoullistrasse 30/32,
kleiner Hörsaal 120 | Christoph
Puetz
|
|
11038-03 | Donnerstag
10h15-12h | Kollegienhaus,
Seminarraum 104 | Marta
Dujella
|
|
11038-04 | Freitag
10h15-12h | Bernoullistrasse 30/32,
kleiner Hörsaal 120 | Gabriel
Dill
|
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein.
Jede Woche gibt es ein Blatt:
|
Standardprogramm: |
Die Aufgaben vom Standardprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Montag, den 16. Dezember 2019, 10.15 - 11.15 Uhr (Alte Uni).
Wiederholungsklausur: 30. Januar 2020, 10.15 - 11.15 Uhr (Alte Uni).
|
Ergänzungsprogramm:
|
Die Aufgaben vom Ergänzungsprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Montag, den 16. Dezember 2019, 11.30 -12.30 Uhr (Alte Uni).
Wiederholungsklausur: 30. Januar 2020, 11.30 - 12.30 Uhr (Alte Uni).
|
Die Resultaten der Klausur werden am Dienstag, den 17. Dezember 2019, gegeben sein.
Auszug aus der Literatur:
|
G. Fischer | Lineare Algebra. | Vieweg Verlag.
|
FS19 - MASTERVERTIEFUNGSMODUL:
Algebraische Geometrie II
Algebraische Geometrie studiert geometrische Objekte, die als Lösungen von Polynomgleichungen definiert sind. Viele bekannte geometrische Objekte können als Lösungsmenge von geeigneten Polynomgleichungen beschrieben werden: Kreise, Kugeln, Hyperbeln,...
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistentin: | Julia Schneider --
julia noemi noemi schneider schneider  unibas unibas ch ch
|
|
Vorlesung: | Dienstag 14.15 -16.00 Uhr (Spiegelgasse 5, Seminarraum 05.001)
Mittwoch 10.15 -12.00 Uhr (Spiegelgasse 5, Seminarraum 05.001)
|
|
Klausur: |
Dienstag, 4 Juni 2019, 10.15 -12.00 Uhr (Spiegelgasse 5, Seminarraum 05.001)
|
|
Übungen: | Donnerstag 14.15 -16.00 Uhr (Spiegelgasse 5, Seminarraum 05.001)
|
|
|
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein.
Auszug aus der Literatur:
|
M. Reid | Undergraduate algebraic geometry. | London Mathematical Society Student Texts.
| |
I. R. Shafarevich | Basic algebraic geometry. 1.+ 2. | Springer.
| |
K. Hulek | Elementare Algebraische Geometrie. | vieweg studium, Aufbaukurs Mathematik.
|
|
W. Fulton | Algebraic curves. | Web page of W. Fulton.
|
|
G. Fischer | Ebene algebraische Kurven. | vieweg studium, Aufbaukurs Mathematik.
| |
R. Hartshorne | Algebraic geometry. | Springer.
| |
M. Brodman | Algebraische Geometrie - Eine Einführung. | Basler Lehrbücher - Birkhauser
|
FS18 - Grundstudium: LINEARE ALGEBRA II
In dieser Lehrveranstaltung, wie in Lineare Algebra I behandeln wir die Grundlagen der linearen Algebra, welche in allen weiterführenden
Vorlesungen und Seminaren in Mathematik und Physik vorausgesetzt werden.
Behandelt werden in diesem Semester Tensorprodukten, Exteriorprodukten, Determinante, Konjugationsklassen, Normalformen, Eigenvektoren, Diagonalisierbarkeit, Bilinearformen,...
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Linda Frey, Stefan Schmid, Julia Schneider, Aline Steiner |
|
Vorlesung: | Montag 8.15 -10.00 Uhr, Kollegienhaus, Hörsaal 116 (Petersplatz 1, Basel)
Dienstag 8.15 -10.00 Uhr, Alte Universität, Hörsaal 101 (Rheinsprung 9, Basel) |
|
Übungen: |
|
11040-03 | Mittwoch
10h15-12h | Bernoullianum 32,
kleiner Hörsaal 120 | Julia
Schneider
|
|
11040-01 | Donnerstag
10h15-12h | Kollegienhaus,
Seminarraum 104 | Stefan
Schmid
|
|
11040-04 | Donnerstag
10h15-12h | Kollegienhaus,
Seminarraum 107 | Aline
Steiner
|
|
11040-02 | Freitag
10h15-12h | Pharmazie-Historisches Museum
Grosser Hörsaal | Linda
Frey
|
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein.
Jede Woche gibt es ein Blatt:
|
Standardprogramm: |
Die Aufgaben vom Standardprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Montag, den 28. Mai 2018, 7.45 - 8.45 Uhr.
|
Ergänzungsprogramm:
|
Die Aufgaben vom Standardprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Montag, den 28. Mai 2018, 9.00 -10.00 Uhr.
|
Auszug aus der Literatur:
|
G. Fischer | Lineare Algebra. | Vieweg Verlag.
| |
M. Artin | Algebra | Birkhäuser Verlag.
|
HS17 - Grundstudium: LINEARE ALGEBRA I
In dieser Lehrveranstaltung und ihrer Fortsetzung im Frühjahrsemester 2018
behandeln wir die Grundlagen der linearen Algebra, welche in allen weiterführenden
Vorlesungen und Seminaren in Mathematik und Physik vorausgesetzt werden.
Behandelt werden in diesem Semester Gruppen, Vektorräume, lineare
Gleichungssysteme, Matrizen und lineare Abbildungen.
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Sebastian Bruggmann, Luzia Felber, Alexander Heinimann, Julia Schneider, Aline Steiner |
|
Vorlesung: | Montag 8.15 -10.00 Uhr, Kollegienhaus, Hörsaal 117 (Petersplatz 1, Basel)
Dienstag 8.15 -10.00 Uhr, Alte Universität, Hörsaal 101 (Rheinsprung 9, Basel) |
|
Übungen: |
|
11038-01 | Mittwoch
10h15-12h | Spiegelgasse 1,
Seminarraum 00.003 (EG) | Aline
Steiner
|
|
11038-02 | Donnerstag
10h15-12h | Kollegienhaus,
Seminarraum 105 | Alexander
Heinimann
|
|
11038-05 | Donnerstag
10h15-12h | Kollegienhaus,
Seminarraum 104 | Sebastian
Bruggmann
|
|
11038-03 | Freitag
10h15-12h | Kollegienhaus,
Seminarraum 106 | Julia
Schneider
|
|
11038-04 | Freitag
10h15-12h | Kollegienhaus,
Seminarraum 208 | Luzia
Felber |
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein.
Jede Woche gibt es ein Blatt:
|
Standardprogramm: |
Die Aufgaben vom Standardprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Dienstag, den 19. Dezember 2017, 7.45 - 8.45 Uhr.
|
Ergänzungsprogramm:
|
Die Aufgaben vom Standardprogramm müssen aufgeschrieben und abgegeben werden (75 % von den Blätter).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Dienstag, den 19. Dezember 2017, 9.00 -10.00 Uhr.
|
Auszug aus der Literatur:
|
G. Fischer | Lineare Algebra. | Vieweg Verlag.
| |
M. Artin | Algebra | Birkhäuser Verlag.
|
HS16 + FS17 - MASTERVERTIEFUNGSMODUL:
Algebraische Geometrie I + II
Algebraische Geometrie studiert geometrische Objekte, die als Lösungen von Polynomgleichungen definiert sind. Viele bekannte geometrische Objekte können als Lösungsmenge von geeigneten Polynomgleichungen beschrieben werden: Kreise, Kugeln, Hyperbeln,...
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein. Jeder Student muss auch einmal an die Tafel gehen und eine Aufgabe vorlösen.
Auszug aus der Literatur:
|
M. Reid | Undergraduate algebraic geometry. | London Mathematical Society Student Texts.
| |
I. R. Shafarevich | Basic algebraic geometry. 1.+ 2. | Springer.
| |
K. Hulek | Elementare Algebraische Geometrie. | vieweg studium, Aufbaukurs Mathematik.
|
|
W. Fulton | Algebraic curves. | Web page of W. Fulton.
|
|
G. Fischer | Ebene algebraische Kurven. | vieweg studium, Aufbaukurs Mathematik.
| |
R. Hartshorne | Algebraic geometry. | Springer.
| |
M. Brodman | Algebraische Geometrie - Eine Einführung. | Basler Lehrbücher - Birkhauser
|
FS16 - Aufbaustudium: KOMMUTATIVE ALGEBRA
In dieser Vorlesung werden wir kommutative Ringe und Moduln über kommutative Ringe studieren (Exakte Folgen, Projektive und Injektive Moduln, Noethersche Moduln, Tensorprodukten, Dimension von Krull, ...).
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Mattias Hemmig, Andrea Fanelli
|
|
Vorlesung: | Montag 10.15 -12.00 Uhr (Spiegelgasse 5, Seminarraum 05.002)
Dienstag 10.15 -12.00 Uhr (Spiegelgasse 1, Seminarraum 00.003)
|
|
Klausur: |
30 Mai 2016, 10h15 in Spiegelgasse 5, Seminarraum 05.002.
|
|
Mündliche Prüfung: |
August 2016, Spiegelgasse 1 (5. Stock, 05.006).
|
|
Übungen: |
|
Mittwoch | 08h15-10h00 | Spiegelgasse 5, Seminarraum 05.001 | Mattias Hemmig |
|
Donnerstag | 14h15-16h00 | Spiegelgasse 5, Seminarraum 05.001 | Andrea Fanelli |
Blatt 1 Blatt 2 Blatt 3
Blatt 4
Blatt 5
Blatt 6
Blatt 7
Blatt 8
Blatt 9
Blatt 10
Blatt 11
Blatt 12
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein. Jeder Student muss auch einmal an die Tafel gehen und eine Aufgabe vorlösen.
Auszug aus der Literatur:
Atiyah, M. F., I. G. Macdonald, Introduction to Commutative Algebra
Matsumura, Commutative Ring Theory
R. Brüske, F. Ischebeck, F. Vogel Kommutative Algebra
(Matsumura, Commutative algebra)
|
FS16 - PROSEMINAR: Geometrie
Das Proseminar ist über klassiche Geometrie. Wir werden dem Buch "Geometry: Euclid and beyond" von R. Hartshorne folgen.
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistentin: | Carla Grolimund --
Carla grolimund grolimund  unibas unibas ch ch |
|
Zeit und Ort: | Freitag 8.15 -10.00 Uhr, Seminarraum 05.001 (Spiegelgasse 5, Basel) |
|
Programm: |
|
26.02.2016: | Vorbesprechung und Verteilung der Vorträge (um 9h15) |
|
11.03.2016: |
Yannick Thommen |
§ 3-4
(Seiten 27-51) | Euclid's Axiomatic Method +
Construction of the Regular Pentagon |
|
18.03.2016: | Raphael Erb |
§ 6-9
(S. 66-96) | Hilbert's Axioms (Incidence + Betweenness
+ Congruence for Line Segments + Congruence for Angles) |
|
01.04.2016: | Gerold Schefer |
§ 13-15
(S. 117-140) | Geometry over fields (The Real Cartesian Plane + Abstract
Fields and Incidence + *Ordered Fields and Betweenness) |
|
15.04.2016: | Patrizia Marquis |
§ 28-31
(S. 241-280) | Construction problems and field extensions (Three Famous
Problems + *The Regular 17-Sided Polygon + *Constructions with Compass and Marked Ruler +
*Cubic and Quartic Equations) |
|
22.04.2016: | Sabrina Doser |
§ 33-34
(S. 295-319) | Non-Euclidean Geometry (History of the Parallel Postulate + Neutral Geometry) |
|
29.04.2016: | Patrice Meunier |
§ 40
(S. 373-388) | Hyperbolic Geometry |
|
HS15 - Aufbaustudium: ALGEBRA
Die Algebra untersucht allgemeine Strukturen, sie bildet einen fundamentalen Block für alle anderen Gebiete der Mathematik.
In dieser Vorlesung werden wir Ringe studieren (Ringhomomorphismen, Einheiten, Unterringe, Ideale, Polynomringe, Körper, faktorielle Ringe, Hauptidealringen, ...).
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Mattias Hemmig, Patrick Schaffter, Francesco Veneziano
|
|
Vorlesung: | Montag 10.15 -12.00 Uhr (Kollegienhaus, 114)
Dienstag 10.15 -12.00 Uhr (Alte Universität, U201)
|
|
Klausur: |
7 Dezember 2015, 10h15 im Kollegienhaus (114)
|
|
Mündliche Prüfung: |
11-15 Januar 2016, Spiegelgasse 1 (5. Stock, 05.006).
|
|
Wiederholungsklausur: |
25 Januar 2016, 10h15, Spiegelgasse 5 (5. Stock).
|
|
Übungen: |
|
Mittwoch | 08h15-10h00 | Spiegelgasse 1, Seminarraum 00.003 | Mattias Hemmig |
|
Donnerstag | 14h15-16h00 | Kollegienhaus, Seminarraum 208 | Patrick Schaffter |
|
Freitag | 10h15-12h00 | Bernouillanum, 32 | Francesco Veneziano |
Blatt 1 Blatt 2 Blatt 3 Blatt 4 Blatt 5 Blatt 6 Blatt 7 Blatt 8 Blatt 9
Blatt 10
Blatt 11
Blatt 12
Blatt 13
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein. Jeder Student muss auch einmal an die Tafel gehen und eine Aufgabe vorlösen.
Auszug aus der Literatur:
HS14 + FS15 - MASTERVERTIEFUNGSMODUL:
Projektive algebraische Kurven und Flächen I + II
Algebraische Geometrie studiert geometrische Objekten, die als Lösungen von Polynomgleichungen definiert sind. Viele bekannte geometrische Objekte können als Lösungsmenge von geeigneten Polynomgleichungen beschrieben werden: Kreise, Kugeln, Hyperbeln,...
In dieser Vorlesung werden wir Kurven (Geschlecht, Divisoren, Riemann-Roch,...) und Flächen (Aufblasungen, Divisoren mit Durschnittformen,...) studieren.
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein. Jeder Student muss auch einmal an die Tafel gehen und eine Aufgabe vorlösen.
Auszug aus der Literatur:
|
W. Fulton | Algebraic curves. | Web page of W. Fulton.
|
|
K. Hulek | Elementare Algebraische Geometrie. | vieweg studium, Aufbaukurs Mathematik.
|
|
G. Fischer | Ebene algebraische Kurven. | vieweg studium, Aufbaukurs Mathematik.
| |
M. Reid | Undergraduate algebraic geometry. | London Mathematical Society Student Texts.
| |
I. R. Shafarevich | Basic algebraic geometry. 1.+ 2. | Springer.
| |
R. Hartshorne | Algebraic geometry. | Springer.
| |
M. Brodman | Algebraische Geometrie - Eine Einführung. | Basler Lehrbücher - Birkhauser
|
HS13 - Grundstudium: LINEARE ALGEBRA I
In dieser Lehrveranstaltung und ihrer Fortsetzung im Frühjahrsemester 2014 (gelesen bei P.-M. Poloni)
behandeln wir die Grundlagen der linearen Algebra, welche in allen weiterführenden
Vorlesungen und Seminaren in Mathematik und Physik vorausgesetzt werden.
Behandelt werden in diesem Semester Gruppen, Vektorräume, lineare
Gleichungssysteme, Matrizen und lineare Abbildungen.
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistenten: | Anna Bohun, Richard Häni, Andriy Regeta, Maria Fernanda Robayo |
|
Vorlesung: | Montag 8.15 -10.00 Uhr, Kollegienhaus, Hörsaal 115 (Petersplatz 1, Basel)
Dienstag 8.15 -10.00 Uhr, Kollegienhaus, Hörsaal 115 (Petersplatz 1, Basel) |
|
Übungen: |
Montag 10.15-12.00 Uhr, Kollegienhaus, Seminarraum 104 - Anna Bohun
Montag 10.15-12.00 Uhr, Kollegienhaus, Seminarraum 105 - Maria Fernanda Robayo
Donnerstag 10.15-12.00 Uhr, Kollegienhaus, Seminarraum 104 - Andriy Regata
Freitag 10.15-12.00 Uhr, Kollegienhaus, Seminarraum 106 - Richard Häni
|
Zur Erlangung der Kreditpunkte müssen die Übungen sinnvoll bearbeitet sein und die Klausur bestanden sein.
Jede Woche gibt es ein Blatt:
|
Standardprogramm: |
Aufgabe 1 und 2: müssen aufgeschrieben und abgegeben werden (80 %).
Aufgabe 3 und 4: müssen nur bearbeitet und nicht abgegeben werden. Werden an der Tafel von der Studierenden vorgelöst (mindestens zweimal pro Semester pro Student).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Dienstag, den 10. Dezember 2013, 7.45 - 8.45 Uhr.
|
Ergänzungsprogramm:
|
Aufgabe 5: muss aufgeschrieben und abgegeben werden (80 %).
Aufgabe 6: muss nur bearbeitet und nicht abgegeben werden. Wird an der Tafel von der Studierenden vorgelöst (mindestens einmal pro Semester pro Student).
Die Studierende müssen eine einstündige schriftliche Klausur am Ende des Semesters bestehen,
und zwar am Dienstag, den 10. Dezember 2013, 9.00 -10.00 Uhr.
|
Probeklausur
Das Kalender ist wie folgt:
|
|
Datum des neuen Blattes
|
Abgabedatum
Übungsgruppen
von Donnerstag / Freitag | Übungsgruppen
von Montag |
|
Blatt 0
Blatt 1
Blatt 2
Blatt 3
Blatt 4
Blatt 5
Blatt 6
Blatt 7
Blatt 8
Blatt 9
Blatt 10
Blatt 11 |
17.09.2013
24.09.2013
01.10.2013
08.10.2013
15.10.2013
22.10.2013
29.10.2013
05.11.2013
12.11.2013
19.11.2013
26.11.2013
17.12.2013
|
keine Abgabe
01.10.2013
08.10.2013
15.10.2013
22.10.2013
29.10.2013
05.11.2013
12.11.2013
19.11.2013
26.11.2013
03.12.2013
keine Abgabe
| keine Abgabe
03.10.2013
10.10.2013
17.10.2013
24.10.2013
31.10.2013
07.11.2013
14.11.2013
21.11.2013
28.11.2013
05.12.2013
keine Abgabe
|
|
Wiederholungsklausur (Im Kollegienhaus, Hörsaal 118):
|
STANDARDPROGRAMM: | Donnerstag, den 16. Januar 2014, 9.45 -10.45 Uhr. |
|
ERGÄNZUNGSPROGRAMM: | Donnerstag, den 16. Januar 2014, 11.00 -12.00 Uhr. |
Auszug aus der Literatur:
|
G. Fischer | Lineare Algebra. | Vieweg Verlag.
| |
M. Artin | Algebra | Birkhäuser Verlag.
|
FS13 - MASTERKURS: Gruppenkohomologie
Ich habe die Kohomologiemengen H0(G,A) und H1(G,A) definiert, wenn G eine Gruppe ist, die auf einer anderen Gruppe A operiert. Und auch die Kohomologiegruppen Hn(G,A) für jedes n, wenn A abelsch ist.
Wir haben gelernt, wie man Kohomologiemengen berechnet (mit Hilbert 90 und exakten Folgen) und haben Anwendungen dieser Mengen in der Gruppen-, Algebren- und Zahlentheorie studiert.
Auszug aus der Literatur:
|
S. Bosch | Algebra. | Springer.
| |
I. R. Shafarevich | Algebra I. | Springer.
| |
J.-P. Serre | Local fields. | Springer.
|
HS12 - SEMINAR: Geometrische Gruppentheorie
Das Seminar ist eine Einführung in die Geometrische Gruppentheorie. Wir haben einige Seiten von dem Buch "Topics in geometric group theory" von P. de La Harpe gelesen.
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistent: | Pierre-Marie Poloni --
pierre-marie poloni poloni  unibas unibas ch ch |
|
Zeit und Ort: | Mittwoch 8.15 -10.00 Uhr, Kleiner Hörsaal (Rheinsprung 21, Basel) |
|
Programm: |
|
18.09.2012: | Vorbesprechung und Verteilung der Vorträge |
|
03.10.2012: | Carlo Seppi und Oliver Niklaus | Weight on a group |
|
10.10.2012 : | Viviane Wehrle und Aline Steiner | Polya's reccurence theorem (random walk on 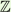 m) m) |
|
17.10.2012: | Fabio Thöny und Christine Bürli | Free groups |
|
24.10.2012: | Nikola Ilic und Antal Horváth | Free groups as groups acting freely on trees |
|
7.11.2012: | Gabriel Dill und Lukas Ehlers | Table tennis lemma (Klein's criterion) and examples of free products |
|
14.11.2012: | Adrian Denz | Fundamental groups and free products |
|
21.11.2012: | Richard Haeni und Matthias Bleile | Finitely generated groups |
|
28.11.2012 | Julia Kopp und Ilana Fried | Examples of free groups |
| 5.12.2012:
| Zoé Zarri und Maurus Thurneysen | Exercises on finitely generated groups |
|
12.12.2012: | Susanna Zimmermann | Word length and Quasi-Isometries |
|
HS11 - MASTERVERTIEFUNGSMODUL:
Kommutative Algebra - I
Die Kommutative Algebra ist die Theorie der kommutativen Ringe und der
Moduln über diesen.
Ich habe erste Semester gelesen. Elisa Gorla hat zweite Semester gelesen.
Grösse Hörsaal
Assistent: Emilie Dufresne
Studenten:
|
| Aeschlimann | Andreas | |
Heule | Stephan | |
Horvath | Antal | |
Ilic | Nikola | |
Lützelschwab | Lars | |
Matter | Niels | |
Schulze | Christian | |
| |
Kleiner Hörsaal
Assistent: Immanuel Stampfli
Studenten:
|
| Filipovic | Sanja | |
Häni | Richard | |
Matthäus | Maximilian | |
Oberlin | Irina | |
Rohr | Stephanie | |
Seiler | Alexander | |
Zimmermann | Susanna | |
|
Zur Erlangung der Kreditpunkte (8 KP) müssen die Übungen schriftlich bearbeitet und abgegeben werden, und man muss zur Vorlesung und zu den Übungen gehen. Jeder Student muss auch zweimal an die Tafel gehen und eine Aufgabe vorlösen.
Auszug aus der Literatur:
|
M.F. Atiyah, I.G. MacDonald | Introduction to commutative algebra. | Addison-Wesley Publishing Co., Reading
| |
R. Brüske, F. Ischebeck, F. Vogel | Kommutative Algebra | Bibliographisches Institut, Mannheim.
| |
D. Eisenbud | Commutative algebra
with a view toward algebraic geometry. | Graduate Texts in Mathematics. Springer.
|
FS11 - MASTERKURS: Geometrie der projektiven algebraischen Flächen
Ich habe eine Einführung in die projektive algebraische Geometrie geben, und dann mehr über projektiven algebraischen Flächen gesprochen.
Auszug aus der Literatur:
|
K. Hulek | Elementare Algebraische Geometrie. | vieweg studium, Aufbaukurs Mathematik.
| |
G. Fischer | Ebene algebraische Kurven. | vieweg studium, Aufbaukurs Mathematik.
| |
M. Reid | Undergraduate algebraic geometry. | London Mathematical Society Student Texts.
| |
I. R. Shafarevich | Basic algebraic geometry. 1.+ 2. | Springer.
| |
R. Hartshorne | Algebraic geometry. | Springer.
| |
M. Brodman | Algebraische Geometrie - Eine Einführung. | Basler Lehrbücher - Birkhauser
|
HS10 - SEMINAR: Projektive Geometrie
Das Seminar war eine Einführung in die algebraische Geometrie der Kurven in der projektiven Ebene. Wir haben Kapitel II von dem Buch "Ebene algebraische Kurven" von E. Brieskorn/H. Knörrer gelesen.
|
Dozent: | Jérémy Blanc --
jeremy blanc blanc  unibas unibas ch ch |
|
Assistent: | Alexandru Constantinescu --
a constantinescu constantinescu  unibas unibas ch ch |
|
Zeit und Ort: | Montag 10.15 -12.00 Uhr, Seminarraum (Rheinsprung 21, Basel) |
|
Programm: |
|
23.09.2010: | Vorbesprechung und Verteilung der Vorträge |
|
04.10.2010: | Jérémy Blanc | Einführung (Algebraische kurven, die projektive Ebene,...) |
|
11.10.2010 : | Stephan Heule | Zerlegung in irreduziblen Komponenten (257-265) |
|
18.10.2010: | Susanna Zimmermann | Nullstellen von Polynomen (240-256) |
|
25.10.2010: | Nikola Ilic | Resultante (222-232) |
|
5.11.2010: | Fabian Müller | Singuläre Punkte ebener Kurven (269-273 und 288-291) |
|
8.11.2010: | Elena Frankel | der Satz von Bézout (291-304) |
|
15.11.2010: | Mirjam Laager | Linearsystemen (305-313) |
|
22.11.2010: | Tiziana Radici | der Satz von Pascal (314-319) |
|
29.11.2010: | Christian Urech | Dualitätprinzip und der Satz von Brianchon (321-331) |
|
13.12.2010: | Mattias Hemmig | Quadriken / Kubiken (359-366) |
|
20.12.2010: | Filip Misev | Wendepunktfigur und Normalform von Kubiken (359-379) |
|
|
 unibas
unibas