Workshop:
Algebraic Transformation Groups

May 5-8, 2024 - Monte Verità Ascona, Switzerland

The workshop is devoted to the most recent results centered around algebraic transformation groups. This will bring together people from affine and birational geometry, as well as representation theory and complex geometry. The workshop takes place in Monte Verità, a beautiful place in southern Switzerland. Here is some short movie about the Monte Verità.

Here you can find practical information for the venue. There will be a shuttle taxi from the train station in Locarno to Monte Verità on 5 May at 11:00, 11:40, 12:20, 13:00, 13:40, 14:20. For the journey back on 8 May, there will be again a taxi shuttle to Locarno. This will be organised during the workshop. The address of the hotel is:

Fondazione Monte Verità
Strada Collina 84
CH-6612 Ascona
Tel. +41 91 785 40 40
info@monteverita.org

The talks will take place in the Auditorium. More information can be found here .

Speakers:

Ivan ARZHANTSEV - HSE University
Karin BAUR - University of Leeds
Anna BOT - Universität Basel
Michel BRION - Université Grenoble Alpes
Serge CANTAT - Université de Rennes
Jean-Philippe FURTER - Université de Bordeaux
Neena GUPTA - Indian Statistical Institute
Friedrich KNOP - Universität Erlangen-Nürnberg
Frank KUTZSCHEBAUCH - Universität Bern
Stéphane LAMY - Université de Toulouse
Peter LITTELMANN - Universität zu Köln
Lucy MOSER-JAUSLIN - Université de Bourgogne
Gerry SCHWARZ - Brandeis University
Susanna ZIMMERMANN - Université Paris-Saclay

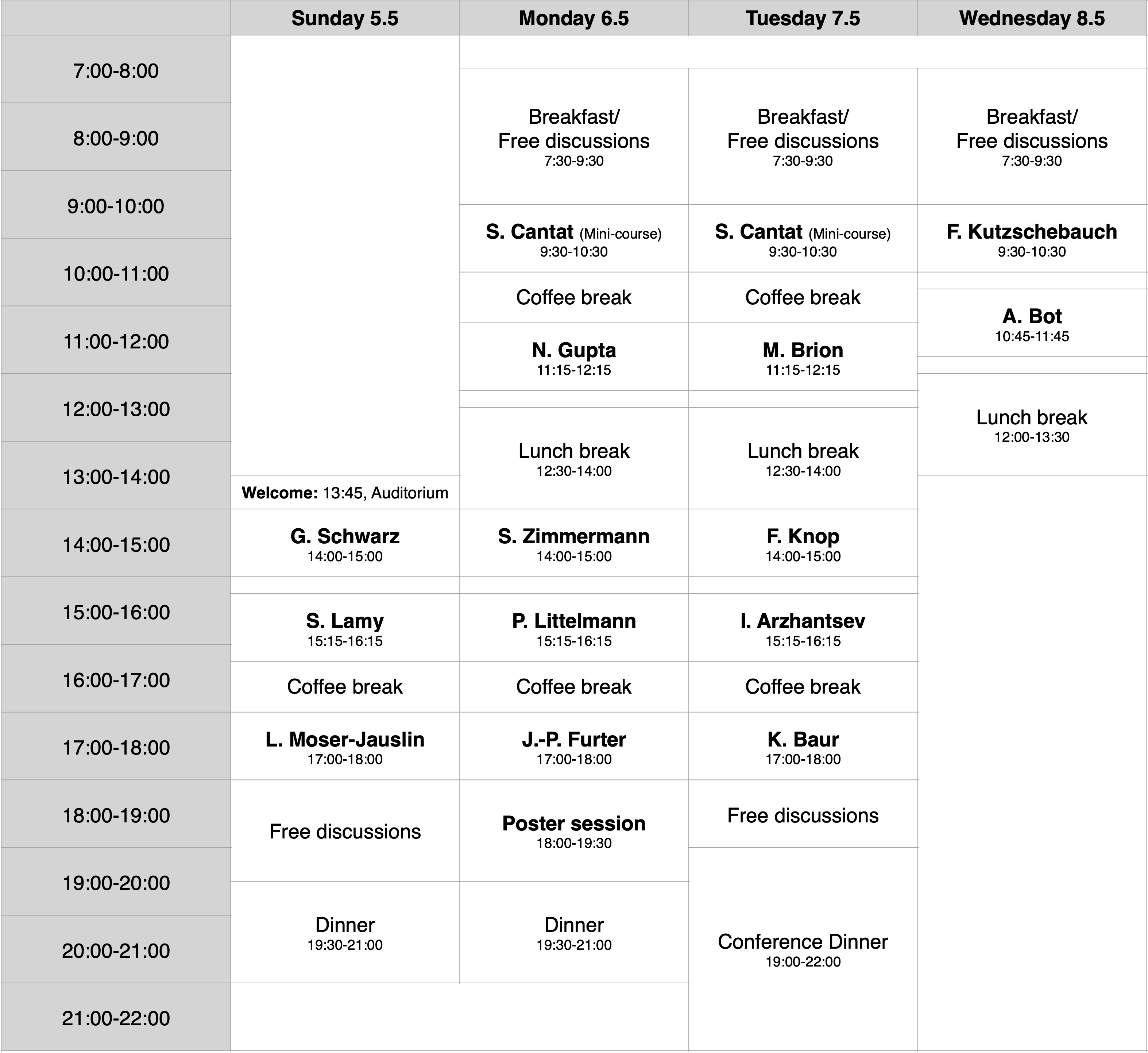
Schedule:

Participants:

Marc Abboud - Université de Neuchâtel
Rafael Andrist - University of Ljubljana
Ivan Arzhantsev - HSE University
Karin Baur - Ruhr-Universität Bochum
Cinzia Bisi - Università degli Studi di Ferrara
Jérémy Blanc - Université de Neuchâtel
Anna Bot - Universität Basel
Michel Brion - Université Grenoble Alpes
Serge Cantat - Université de Rennes
Michael Chitayat - Université d'Ottawa
Daniel Daigle - Université d'Ottawa
Corrado de Concini - Università di Roma
Jan Draisma - Universität Bern
Andrea Fanelli - Université de Bordeaux
Gene Freudenburg - Western Michigan University
Jean-Philippe Furter - Université de Bordeaux
Parnashree Ghosh - Indian Statistical Institute
Neena Gupta - Indian Statistical Institute
Alicia Jaquet-Chiffelle - Université de Neuchâtel
Friedrich Knop - Universität Erlangen-Nürnberg
Hanspeter Kraft - Universität Basel
Frank Kutzschebauch - Universität Bern
Stéphane Lamy - Université de Toulouse
Peter Littelmann - Universität zu Köln
Lucy Moser-Jauslin - Université de Bourgogne
Antoine Pinardin - University of Edinburgh
Claudio Procesi - Università di Roma
Andriy Regeta - Universität Jena
Anne Schnattinger - Université de Neuchâtel
Julia Schneider - Universität Zürich
Gerry Schwarz - Brandeis University
Christian Urech - ETH Zürich
Alain Valette - Université de Neuchâtel
Immanuel van Santen - Universität Basel
Henrik Wehrheim - Université de Neuchâtel
Egor Yasinsky - Université de Bordeaux
Susanna Zimmermann - Université Paris-Saclay

Titles and abstracts of the talks:

Ivan Arzhantsev
Flexible varieties, images of affine spaces, and ellipticity after Mikhail Gromov

We define flexible affine algebraic varieties, describe their basic properties, and show that many varieties satisfy the flexibility condition. The group of special automorphisms acts in the regular locus of a flexible variety infinitely transitively, that is, any finite collection of smooth points can be sent to any finite collection of smooth points of the same cardinality. Using flexibility, we show that every non-degenerate toric variety, every homogeneous space of a semisimple group, and every variety covered by affine spaces admits a surjective morphism from an affine space. Applying the ellipticity property introduced by Mikhail Gromov in 1989, we prove that a complete algebraic variety X is an image of an affine space if and only if X is unirational. This result is obtained in a joint work with Shulim Kaliman and Mikhail Zaidenberg.

Karin Baur
Cluster structures via surface combinatorics

Surface combinatorics have been instrumental in describing algebraic structures such as cluster algebras and cluster categories, gentle algebras, etc. In this talk, I will show how this yields combinatorial approaches to cluster structures on the coordinate ring of the Grassmannians. I will also point out a link to root systems associated to the Grassmannian cluster categories.

Anna Bot
Embeddings of 𝔸2 in 𝔸3 of degree 4 and wild automorphisms

The famous Nagata automorphism is the first example of a wild automorphism of 𝔸3. Wild automorphisms of 𝔸n are the ones that cannot be generated by affine and triangular automorphisms. As the Nagata automorphism is of degree 5, one can wonder whether there exists a wild automorphism of smaller degree. Blanc and van Santen proved that all automorphisms of degree ≤ 3 are tame. Starting from this, I will discuss work in progress on the situation in degree 4 using embeddings of 𝔸2 in 𝔸3 of degree 4.

Michel Brion
Equivariant normalization

Let A be a finitely generated domain over a field of characteristic p. If A is graded by an abelian group M, then the integral closure of A is also M-graded when M is p-torsion free. But this fails when M has p-torsion, for example when M = Z/pZ and A = k[x,y]/(yp - f(x)), where x has degree 0, y has degree 1 and f is a "general" polynomial. More generally, an action of a finite group scheme on a variety need not lift to an action on the normalization. The talk will discuss a notion of equivariant normalization that remedies this problem, and present applications to smooth affine surfaces with an action of the multiplicative group and smooth projective surfaces with an action of an elliptic curve.

Serge Cantat
Automorphisms of affine surfaces and p-adic dynamics

I will describe a general result concerning closures of orbits of groups acting on affine varieties over p-adic fields, and then apply it in the case of surfaces. This is joint work with Seung uk Jang.

Jean-Philippe Furter
Families of Cremona transformations

A family of Cremona transformations is a « morphism » from an algebraic variety to the Cremona group. Such « morphisms » have been defined by Demazure and Serre. In this talk, we will give a few examples of families of Cremona transformations and we will also give some general properties of them (for example related with the length, the dynamical degree, the homaloidal type).

Neena Gupta
The Abhyankar-Sathaye Epimorphism Conjecture

In a famous survey paper published in 1996, Professor H. Kraft compiled a list of eight challenging problems on Affine n-spaces, including the Zariski Cancellation Problem and the Embedding Problem.

The Zariski Cancellation Problem, which asks whether the affine n-space is cancellative, has an affirmation solution for n = 1 and n = 2 and the speaker had shown that in positive characteristic, the affine n-space is not cancellative when n > 2.

In characteristic zero, the Embedding Problem has an affirmative solution when n = 2; it is the famous Epimorphism Theorem of Abhyankar-Moh and Suzuki. The Abhyankar-Sathaye Conjecture, a special case of the Embedding problem, asserts that any embedding of the affine (n-1)-space in affine n-space is rectifiable for any integer n ≥ 3. The problem is open in general. When n = 3, any linear plane was shown to be a coordinate by Sathaye (in characteristic zero) and Russell (in general). The speaker's work on the Zariski Cancellation Problem has opened up investigations on the conjecture for linear hyperplanes in higher dimensions.

In this talk we shall present a few examples of linear hyperplanes where the Abhyankar-Sathaye Conjecture holds. These are based on joint works with Parnashree Ghosh and Ananya Pal.

Friedrich Knop
Multiplicities and dimensions in enveloping tensor categories

To every finitely powered regular category one can attach a family of symmetric tensor category, generalizing the calculus of relations. Under certain conditions these categories are semisimple, hence abelian. In the talk we explain how to compute the dimension of the simple objects and how to decompose the tensor product of simple objects.

Frank Kutzschebauch
Factorization of holomorphic matrices

Every complex symplectic matrix in Sp_2n(ℂ) can be factorized as a product of the following types of unipotent matrices (in interchanging order).

(i): $[\begin{matrix} I & B \\ 0 & I \end{matrix}]$ , upper triangular with symmetric B = B^T.

(ii): $[\begin{matrix} I & 0 \\ C & I \end{matrix}]$ , lower triangular with symmetric C = C^T.

The optimal number T(ℂ) of such factors that any matrix in Sp_2n(ℂ) can be factored into a product of T factors has recently been established to be 5 by Jin, P. Lin, Z. and Xiao, B.

If the matrices depend continuously or holomorphically on a parameter, equivalently their entries are continuous functions on a topological space or holomorphic functions on a Stein space X, it is by no means clear that such a factorization by continuous/holomorphic unipotent matrices exists. A necessary condition for the existence is the map X → Sp_2n(ℂ) to be null-homotopic. This problem of existence of a factorization is known as the symplectic Vaserstein problem or Gromov-Vaserstein problem. In this talk we report on the results of the speaker and his collaborators B. Ivarsson, E. Low and of his Ph.D. student J. Schott on the complete solution of this problem, establishing uniform bounds T(d, n) for the number of factors depending on the dimension of the space d and the size n of the matrices.

It seems difficult to establish the optimal bounds. However we obtain results for the numbers T(1, n), T(2, n) for all sizes of matrices in joint work with our Ph.D. students G. Huang and J. Schott and B.Tran.

Finally we give an application to the problem of writing holomorphic symplectic matrices as product of exponentials.

Stéphane Lamy
Tame polynomial automorphisms acting on spaces with nonpositive curvature

The group Tame(𝔸n) of tame automorphisms is the subgroup of polynomial automorphisms of the affine space generated by linear automorphisms and elementary automorphisms (these being the ones affecting only one variable). Focusing on the case of three variables, I will explain the contructions of two spaces with negative curvature on which Tame(𝔸3) acts. This allows to obtain some results about this group such as: existence of many normal subgroups, linearizability of finite subgroups, and the Tits alternative. (Based on 3 papers in collaboration with Piotr Przytycki).

Peter Littelmann
On Seshadri stratifications

A Seshadri stratification of an embedded projective variety X ⊆ ℙ(V) can be thought of as a tool generalizing Newton-Okounkov theory. We will explain what these stratifications and report on applications and examples.

If the singular locus of the variety X is of codimension at least two, then there exists always at least one Seshadri stratification, The existence of such a stratification leads to flat degeneration of X into a union of toric varieties X0.

In the case of an embedded flag variety, one can define a Seshadri stratification such that the path model of a representation can be interpreted as a collection of vanishing multiplicities.

The talk is based on joint work with Rocco Chirivì (Lecce) and Xin Fang (Aachen) [CFL].

Lucy Moser-Jauslin
Real forms of almost homogeneous G-varieties

In this talk, we will discuss the classification of real forms of almost homogeneous complex varieties under the action of a reductive group. We start with the case of homogeneous forms, and then, using the combinatorial Luna-Vust theory, show how one can deduce results for the almost homogeneous case. By studying the real points of these varieties, for some cases, we can deduce results about the rationality of the associated real forms. We will also look into generalizations for other perfect fields. This work is in collaboration with R. Terpereau and L. Moulin.

Gerry Schwarz
When does the zero fiber of a moment map have rational singularities?

Let G be a complex reductive group with Lie algebra 𝔤 and let V be a G-module. There is a natural moment mapping μ: V ⊕ V *→ 𝔤* and we denote μ-1(0) by N. We find criteria on V for N to have rational singularities. These criteria fail only if V is "small." In the important special case V = p𝔤 (the direct sum of p copies of 𝔤), N has rational singularities if p ≥ 2. This fact has many consequences. For example, it determines bounds on the growth of the dimensions of irreducible representations of arithmetic subgroups of G. This is joint work with H.-C. Herbig and C. Seaton.

Susanna Zimmermann
Connected algebraic groups acting birationnally on the real plane

Any connected algebraic group acting faithfully by birational transformations on a projective space is a linear group. But who are they? They have been classified up to conjugation by birational maps when they act on the plane or the complex space. In this talk I will explain part of the classification of the ones acting on the real plane. This is work in progress with Ronan Terpereau.