|
Arnaud BEAUVILLE - Finite subgroups of PGL(2,K) |
| We describe the conjugacy classes of finite subgroups of PGL
(2,K), for an arbitrary field K. |
|
Michel BRION - Homogeneous bundles over abelian varieties |
| Given an algebraic variety X equipped with the action of
an algebraic group G, a principal bundle over X is homogeneous if
it is isomorphic to all of its pull-backs under elements of G.
Generalizing results of Miyanishi and Mukai about homogeneous vector
bundles, we describe the structure of homogeneous principal bundles
over an abelian variety. We reduce their classification to
(difficult) problems of linear algebra. |
|
Serge CANTAT - Recent results on the Cremona Group |
| The Cremona group is the group of birational transformations
of the (complex) projective plane. I shall describe how hyperbolic
geometry and geometric group theory can be used to study the
algebraic structure of this group, and show that this group is not simple, as an abstract group. |
|
Pierre DE LA HARPE - Dénombrements d'actions de groupes sur les ensembles finis
et sur les espaces vectoriels |
|
L'exposé décrira deux programmes de comptage
de certaines actions de certains groupes.
D'abord, compter les actions par permutations sur les ensembles finis,
ce qui revient à compter les sous-groupes d'indice fini selon leurs
indices.
Ensuite, compter les représentations linéaires irréductibles
selon leurs dimensions.
Les comptages du premier type sont notamment motivés par
des questions de géométrie riemannienne.
L'intérêt pour les comptages du second type est plus récent
(Witten, Lubotzky, ...)
et sera l'occasion d'énoncer un résultat
obtenu en collaboration avec Laurent Bartholdi. |
|
Hanspeter KRAFT - Affine Space Bundles and Linearization |
| The linearization problem asks if an action of a reductive algebraic group on complex affine n-space An is equivalent to a linear representation. For A2 this is indeed the case, due to the structure of the automorphism group of A2 as an amalgamated product. However, it does not hold in dimension >2.
The first counterexamples were given by G. W. Schwarz in 1989; they initiated an interesting development. A related object in this setting are affine space bundles, i.e. morphisms with all fibers isomorphic to affine n-space. Here the fundamental question is if such a morphism is locally trivial in some reasonable sense. We will describe some highlights, some open problems and some recent developments. |
|
Domingo LUNA - Examples of pseudo-spherical subgroups |
| Let G be a (complex) semi-simple group, B a Borel subgroup of G , and
U the unipotent radical of B . An algebraic subgroup H of G is called
"spherical", if B has an open orbit in G/H ; H spherical implies
dim(H) ≥ dim(U) .
In my talk, I will discuss examples of H's that are not spherical,
although dim(H) ≥dim(U). |
|
Lucy MOSER-JAUSLIN - Isomorphism classes of certain hypersurfaces in complex affine four-space |
| I will discuss work done in collaboration with A. Dubouloz and P.M. Poloni on a set of hypersurfaces of 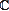 4 having a non-trivial Makar-Limanov invariant. More precisely, we are interested in hypersurfaces defined by an equation of the form xdy+r(x,z,t)=0, where d ≥ 2, and r(0,z,t) satisfies some additional properties. Among these varieties, one finds the Koras-Russell threefolds, which are contractible smooth affine threefolds, endowed with a hyperbolic action of 4 having a non-trivial Makar-Limanov invariant. More precisely, we are interested in hypersurfaces defined by an equation of the form xdy+r(x,z,t)=0, where d ≥ 2, and r(0,z,t) satisfies some additional properties. Among these varieties, one finds the Koras-Russell threefolds, which are contractible smooth affine threefolds, endowed with a hyperbolic action of 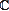 *. They are, in this sense, very similar to affine three-space. We study properties of the automophism groups of these threefolds, and also give some partial results on isomorphisms between such varieties. This study allows us to determine some surprising results about automorphisms of Koras-Russell threefolds. *. They are, in this sense, very similar to affine three-space. We study properties of the automophism groups of these threefolds, and also give some partial results on isomorphisms between such varieties. This study allows us to determine some surprising results about automorphisms of Koras-Russell threefolds. |
|
Raghavan NARASIMHAN - Riemann's Lectures of 1858/59 on the Hypergeometric Series |
| This course of Riemann was written down in "Gabelsberger Stenographie" by Wilhem von Bezold, and came to the attention of the Berlin mathematicians in the 1890's. The aim of this talk is to point out how Riemann had anticipated the ideas of L. Fuchs and H.A. Schwarz and to say a few words about how he proposed studying what we now call finite dimensional local systems of germs of holomorphic functions on 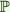 1\ S, where S is a finite set. 1\ S, where S is a finite set. |
Ivan PAN - On Cremona transformations of 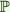 3 with minimal length 3 with minimal length |
| Cremona transformations of the dimension 3 complex projective space may be factorized as a product of elementary links (i.e, elementary birational maps between Mori Fiber Spaces). We classify all Cremona transformations which factorize as a product of m links (without flips) for m ≤ 2. |
|
Gerald SCHWARZ - Characteristic invariants of reductive groups |
| Let G be a reductive complex group and V a finite
dimensional G-module. Associated to G there are various invariant
objects: orbits, fibers of the quotient mapping, invariant polynomial
functions, etc. Following Raïs we say that an object is
characteristic if the subgroup of GL(V) preserving it is
G or at least has identity component contained in G. We discuss
some examples of characteristic objects with special attention to
orbits which are characteristic. For many V it turns out that all
nonzero orbits are characteristic. |
|
Andras SZENES - Quantization of symplectic manifolds and the combinatorics of partition functions |
|
On a polarized compact symplectic manifold endowed with an
action of a compact Lie group, in analogy with geometric invariant
theory, one can define the space of invariant functions of degree k. A
central statement in symplectic geometry, the quantization commutes
with reduction hypothesis, is equivalent to saying that the dimension
of these invariant functions depends polynomially on k. This statement
was proved by Meinrenken and Sjamaar under positivity conditions. In
joint work with Mich¸le Vergne, we found a new proof of this
polynomiality, which is much less technical than the earlier proofs.
In this talk, I will explain the basic ideas of this proof, in which a
prominent role is played by the theory of partition functions. |