|
|
4th Swiss-French workshop on algebraic geometry
Enney (near Gruyères, Fribourg, Switzerland), January 26-30, 2015
The workshop will be held in Enney from January 26 to 30, 2015.
Mini-courses
In the morning, there will be three mini-courses of 5 hours (3 times one hour each day).
Stéphane DRUEL (Grenoble)
|
Rational curves on algebraic varieties |
|
|
|
|
Antoine DUCROS (Paris) |
Introduction to Berkovich spaces
|
|
|
|
|
Stéphane LAMY (Toulouse) |
Transformation groups acting on hyperbolic spaces
|
In the afternoon, we will have research talks of 50 minutes.
Schedule Talks: In Enney, ( "Centre l'Ondine, Viva-Gruyère" )
Monday
January 26
|
Tuesday
January 27
|
Wednesday
January 28 |
Thursday
January 29 |
Friday
January 30 |
12h30 welcome
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
breakfast
8h45-9h45
mini-course 1
10h-11h
mini-course 2
11h15-12h15
mini-course 3
|
| lunch |
lunch |
lunch |
lunch |
|
14h30-15h30
mini-course 1
16h00-17h00
mini-course 2
17h30-18h30
mini-course 3
dinner
|
time for discussion / enjoying the mountain
17h20-18h10
K. Palka
18h30-19h20
M. Benzerga
dinner
|
time for discussion / enjoying the mountain
17h20-18h10
J. Déserti
18h30-19h20
M. Hemmig
dinner
|
time for discussion / enjoying the mountain
17h20-18h10
D. Avritzer
18h30-19h20
A. Lonjou
dinner
|
|
Mini-courses - titles and abstracts
|
Stéphane DRUEL - Rational curves on algebraic varieties |
|
In this course we shall discuss geometric aspects of the theory of rational curves on
algebraic varieties. We will be mainly interested in uniruled varieties, i.e., varieties that
contain rational curves through every point.
Provisional Program:
1. The space of rational curves, dimension estimates. Existence of rational curves.
2. Families of singular rational curves.
3. Characterizations of projective spaces.
|
|
Antoine DUCROS - Introduction to Berkovich spaces |
|
In the sixties, Tate exhibited explicit formulas describing kind of a uniformization of some p-adic elliptic curves, which motivated mathematicians for developing of an analytic geometry over p-adic fields. This can not been carried out through a naive translation of the usual definitions of the complex setting: indeed, p-adic fields are totally disconnected, hence have plenty of locally constant (and a fortiori locally analytic) functions which are not given by a single power series of infinite radius. One thus needs a rather subtle theory to handle them.
The first one was proposed by Tate himself; thereafter, other approaches have been suggested by Raynaud, Berkovich, and Huber.
The purpose of this course is to describe Berkovich's theory. Roughly speaking, it consists in "adding plenty of points" to the naive p-adic analytic spaces in order to get very nice topological properties, like local compactness and local path-connectedness.
It often requires highly technically involved proofs which we will omit most of the time; we will rather focus on explicit, concrete and very basic examples that illustrate well the definitions and basic properties of Berkovich spaces, and especially the way the homotopy type of such a space encodes deep arithmetical information.
We will also make a survey of some striking applications of the theory, in various areas (arithmetic geometry, general algebraic geometry, dynamics...).
|
|
Stéphane LAMY - Transformation groups acting on hyperbolic spaces |
|
The general theme of these lectures will be the study of transformation groups via their action on (often not immediatly obvious) hyperbolic spaces.
Each lecture will focus on a particular group, and several applications will be discussed along the way, such as the classification of finite subgroups, small cancellation theory and existence of quotient, the Tits alternative...
We plan to cover the following examples:
1 - SL(2,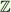 ) acting either on the hyperbolic disk, on its Bass-Serre tree or on ) acting either on the hyperbolic disk, on its Bass-Serre tree or on 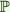 2 as a group of monomial birational maps; 2 as a group of monomial birational maps;
2- The group of polynomial automorphisms Aut(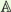 2) acting on its Bass-Serre tree; 2) acting on its Bass-Serre tree;
3- The Mapping Class Group of a Riemann surface acting on the curve complex;
4- The Cremona group Bir(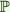 2) acting on an infinite dimensional hyperbolic space; 2) acting on an infinite dimensional hyperbolic space;
5- The group of tame automorphisms of the affine space  3 (resp. of an affine quadric 3-fold) acting on a simplicial complex (resp. a square complex).
Notes of the course 3 (resp. of an affine quadric 3-fold) acting on a simplicial complex (resp. a square complex).
Notes of the course
|
Talks - titles and abstracts
Dan AVRITZER - Linear systems of quadrics in 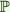 N containing a linear space N containing a linear space |
|
Consider a complete intersection X=Q0∩Q1 of two quadrics in 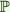 5.
Assume X is nonsingular and
choose a line L⊂X and M≈ 5.
Assume X is nonsingular and
choose a line L⊂X and M≈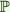 3 disjoint from L. Consider the projection π: 3 disjoint from L. Consider the projection π: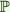 5→M with center L and restrict π to X, this gives a birational map from X to M whose inverse is not defined at the genus two quintic in M given
by a quadric and two cubics.
In a joint paper with I. Pan and G. Gonzalez Sprinberg we applied this to study the Cremona transformations that one obtains from this set up by considering two such projections
and by choosing two such lines.
In this talk, I will explain this and tell about a joint work in progress with C. Peskine where
we are trying to extend this construction by considering a linear system of quadrics in 5→M with center L and restrict π to X, this gives a birational map from X to M whose inverse is not defined at the genus two quintic in M given
by a quadric and two cubics.
In a joint paper with I. Pan and G. Gonzalez Sprinberg we applied this to study the Cremona transformations that one obtains from this set up by considering two such projections
and by choosing two such lines.
In this talk, I will explain this and tell about a joint work in progress with C. Peskine where
we are trying to extend this construction by considering a linear system of quadrics in 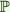 N containing a linear space. Time allowing I will consider an application of this to Fano varieties. N containing a linear space. Time allowing I will consider an application of this to Fano varieties.
|
Mohamed BENZERGA - Real structures on blow-ups of 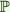 2 2 |
|
A real structure on a complex projective variety X is an antiregular (or antiholomorphic) involution. The data of such a structure on X is equivalent to the data of a real variety whose complexification is isomorphic to X. The aim of this talk is to show how the study of automorphism groups of blow-ups of 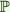 2 can be used in order to give partial answer to the question : is there a finite number of real forms on every blow-up of 2 can be used in order to give partial answer to the question : is there a finite number of real forms on every blow-up of 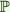 2 up to isomorphism ? 2 up to isomorphism ?
|
|
Julie DESERTI - The group of Cremona maps generated by the standard involution and automorphisms. |
|
In this talk I will give some properties of the group Gn(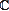 ) of Cremona maps generated by the standard involution and automorphisms. For example I will prove that there is no nontrivial finite dimensional linear representation of Gn( ) of Cremona maps generated by the standard involution and automorphisms. For example I will prove that there is no nontrivial finite dimensional linear representation of Gn(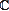 ). ).
|
|
Mattias HEMMIG - Complements of plane curves of low degree |
|
In 1984, Yoshihara conjectured that two irreducible plane curves with isomorphic complements are projectively equivalent. While the conjecture is true for non-rational curves and curves with not exactly one singular point, a counterexample was found by Blanc in 2009. Costa (2010) gave a counterexample in degree 9, which is the lowest known. Our aim is to examine the cases of degree 8 and lower using (-1)-tower resolutions.
|
Anne LONJOU - Non simplicity of the Cremona group Bir(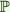 2k), over any field k 2k), over any field k |
|
In 2010, Stéphane Lamy and Serge Cantat proved that if k is an algebraically closed field, the Cremona group is not a simple group by making it act on the Picard-Manin space.
In the same time, Dahmani, Guirardel and Osin established a link between the fact that a group
has an hyperbolic element that satisfies the WPD (weak proper discontinuity) property and the
fact that this group has many normal subgroups.
I'll show that in a hyperbolic space we can weaken the WPD definition and I'll use it to prove that
the Cremona group is not simple over any field k.
|
|
Karol PALKA - On singular embeddings of a complex projective line into the plane |
|
Let E be the image of a singular algebraic embedding of a complex projective line into a projective plane. Since no example with more than 4 singular points is known, people conjectured this is always the case. We will explain our ideas concerning analysis of surfaces of log general type relying on the log MMP with half-integral coefficients. As an appplication we will discuss our proof (with M. Koras) of the conjecture.
|
How to come The journey to Enney is 2 hours from Geneva, 2h30 from Basel/Zurich, 1h30 from Lausanne. See timetables on www.cff.ch.
The train station of Enney is at 10 minutes by foot from the center. See the map, with the blue path given by google (pay attention to the snow!)
Participants
Bachar Al Hajjar (Dijon)
Dan Avritzer (Belo Horizonte)
Mohamed Benzerga (Angers)
Cinzia Bisi (Ferrara)
Jérémy Blanc (Basel)
Alberto Calabri (Ferrara)
Jung-Kyu Canci (Basel)
Julie Déserti (Paris)
Stéphane Druel (Grenoble)
Adrien Dubouloz (Dijon)
Antoine Ducros (Paris)
Jean-Philippe Furter (La Rochelle / Basel)
Isac Hedén (Basel)
Mattias Hemmig (Basel)
Natalia Kolokolnikova (Geneva)
Stéphane Lamy (Toulouse)
Matthias Leuenberger (Bern)
Anne Lonjou (Toulouse)
Frédéric Mangolte (Angers)
Lucy Moser-Jauslin (Dijon)
Charlie Petitjean (Dijon)
Karol Palka (Warsaw)
Alexander Perepechko (Moscow)
Pierre-Marie Poloni (Basel)
Maria Fernanda Robayo (Basel)
Mikhail Shkolnikov (Geneva)
Christian Urech (Basel)
Susanna Zimmermann (Basel)
Send an email to Jeremy  Blanc  unibas  ch if you would like to participate.
Organisers
Adrien Dubouloz (Dijon)
Jérémy Blanc (Basel)




|
 unibas
unibas



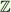 ) acting either on the hyperbolic disk, on its Bass-Serre tree or on
) acting either on the hyperbolic disk, on its Bass-Serre tree or on 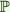
 ) of Cremona maps generated by the standard involution and automorphisms. For example I will prove that there is no nontrivial finite dimensional linear representation of Gn(
) of Cremona maps generated by the standard involution and automorphisms. For example I will prove that there is no nontrivial finite dimensional linear representation of Gn(