|
|
3rd Swiss-French workshop on algebraic geometry
Enney (near Gruyères, Fribourg, Switzerland), January 27-31, 2014
The workshop was held in Enney from January 27 to 31, 2014.
Mini-courses
In the morning, there were three mini-courses of 5 hours (3 times one hour each day).
|
Michel BRION (Grenoble) |
Local properties of actions of linear algebraic groups
|
|
|
|
|
Serge CANTAT (Rennes) |
Dynamical Degrees
|
|
|
|
Yuri PROKHOROV (Moscow)
|
Finite subgroups of the space Cremona group and Fano threefolds. |
In the afternoon, we had research talks of 50 minutes.
Schedule Talks: In Enney, ( "Centre l'Ondine, Viva-Gruyère" )
Monday
January 27
|
Tuesday
January 28
|
Wednesday
January 29 |
Thursday
January 30 |
Friday
January 31 |
12h30 welcome
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
| lunch |
lunch |
lunch |
lunch |
|
14h30-15h30
mini-course 1
16h00-17h00
mini-course 2
17h30-18h30
mini-course 3
dinner
|
time for discussion / enjoying the mountain
17h20-18h10
talk - S. Vishkautsan
18h30-19h20
talk - M. Robayo
dinner
|
time for discussion / enjoying the mountain
17h20-18h10
talk - C. Petitjean
18h30-19h20
talk - J. Furter
dinner
|
time for discussion / enjoying the mountain
17h20-18h10
talk - M. Shkolnikov
18h30-19h20
talk - S. Lamy
dinner
|
|
Mini-courses - titles and abstracts
|
Michel BRION - Local properties of actions of linear algebraic groups |
|
The mini-course will present some fundamental properties
of actions of linear algebraic groups (especially tori) on algebraic
varieties: linearization of invertible sheaves; existence of invariant
affine neighborhoods; the Bialynicki-Birula decomposition. The setting
will be algebraic geometry over an arbitrary field.
|
|
Serge CANTAT - Dynamical Degrees |
|
Let V be a complex projective variety and let f be a rational transformation
of V. The graph G(f) is an algebraic subset of VxV ; taking iterates, one gets a sequence
of graphs G(f^n) in VxV. The dynamical degrees of f are non-negative real numbers
that describe how the sequence G(f^n) grows with n. For instance, they capture
the exponential growth rate of the volume of G(f^n) as n goes to infinity.
I shall explain the definition of these numbers, their dynamical meaning, and some
of the very nice arithmetical properties that they satisfy (at least conjecturally).
|
|
Yuri PROKHOROV - Finite subgroups of the space Cremona group and Fano threefolds |
|
The aim of this course is to introduce a techniques
- based on the minimal model program -
that can be used
to classify finite subgroups of Cremona groups.
I concentrate on the three-dimensional case.
Lecture 1.
Introduction. G-MMP. Fano-Mori models. Examples.
Lecture 2.
Gorenstein Fano threefolds. Projective models. Non-Gorenstein case.
Lecture 3.
Special kinds of Fano threefolds: del Pezzo varieties.
Lecture 4.
Mori-Mukai classification.
Sarkisov links and Fano threefolds of rank 2.
Some invariants of conjugacy classes.
Lecture 5.
Prime Fano threefolds.
Iskovskikh and Mukai classification. Applications.
|
Talks - titles and abstracts
Jean-Philippe FURTER - Generalities on the groups SL2( 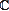 [x1,...,xn] ) [x1,...,xn] ) |
|
The group SL2(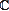 ) is often considered as a good
prototype of a linear algebraic group. Analogously, the theory of ind-groups
should probably begin with groups such as SL2( ) is often considered as a good
prototype of a linear algebraic group. Analogously, the theory of ind-groups
should probably begin with groups such as SL2( 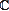 [x1,...,xn] ).
In my lecture, I will address different questions related with these groups,
especially considered as ind-groups. In particular, we will have a look
at the essentially different cases n=1 and n ≥2. [x1,...,xn] ).
In my lecture, I will address different questions related with these groups,
especially considered as ind-groups. In particular, we will have a look
at the essentially different cases n=1 and n ≥2.
|
|
Stéphane LAMY - Blow-up of smooth curves |
|
I will blow-up some smooth curves in threefolds and decide when the variety obtained is weak-Fano. Joint work with JB.
|
|
Charlie PETITJEAN - A combinatorial description of T-varieties |
|
The coordinate ring A of a normal affine variety endowed with an effective action of the torus T=(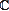 *)n admits a natural grading indexed by the lattice of characters of T. We will review a method due to Altmann and Hausen to describe the graded pieces of A in terms of pairs (Y,D) consisting of a variety Y and a certain divisor D on Y with "combinatorial" coefficients. *)n admits a natural grading indexed by the lattice of characters of T. We will review a method due to Altmann and Hausen to describe the graded pieces of A in terms of pairs (Y,D) consisting of a variety Y and a certain divisor D on Y with "combinatorial" coefficients.
|
|
Maria Fernanda ROBAYO - Finite order birational diffeomorphisms of the sphere for the conic bundle case |
|
Let S be the real algebraic projective surface defined by the equation w2=x2+y2+z2 in 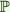 2 2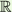 . The group of birational diffeomorphisms of S is denoted by Diffbir(S) or Aut(S( . The group of birational diffeomorphisms of S is denoted by Diffbir(S) or Aut(S(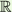 )) and corresponds to those birational transformations f such that f and f -1 are defined at every real point of S.
For g∈Diffbir(S) of finite order it is known that if (X,g') is the minimal resolution of (S,g'), where g'∈Aut(X) is the lift of g, then )) and corresponds to those birational transformations f such that f and f -1 are defined at every real point of S.
For g∈Diffbir(S) of finite order it is known that if (X,g') is the minimal resolution of (S,g'), where g'∈Aut(X) is the lift of g, then
(1) rank Pic(X)g'=1 and X is a Del Pezzo surface, or
(2) rank Pic(X)g'=2 and Π: X→ 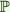 1 is a conic bundle.
We present some algebraic and geometric results about the conjugacy classes of birational diffeomorphisms of finite order for the case (2). 1 is a conic bundle.
We present some algebraic and geometric results about the conjugacy classes of birational diffeomorphisms of finite order for the case (2).
|
|
Mikhail SHKOLNIKOV - Counting curves on surfaces over non-algebraically closed fields |
|
Consider a very ample line bundle on a surface over an algebraically closed field. There is a classical enumerative problem of counting curves in the corresponding linear system of given genus and passing through a generic configuration of points. This numbers are usually called the Severi Degrees, in many cases they are known and well understood. One can try to formulate the same problem over an arbitrary field. But the corresponding number of curves will depend on the configuration of points even if it is generic. In the real case Welschinger managed to define a weighted invariant count of rational curves on a surface. Both Severi Degrees and Welschinger invariants for toric surfaces can be computied in a quite similar way via tropical geometry. Surprisingly, it appears that there exist a one parametric family of such refined invariant tropical counts with so called Bloch-Goettsche multiplicities which in a sense connects real and complex cases. It is expected that they provide answers to some unknown enumerative problems. In my talk I will prose some candidates.
|
|
Soli VISHKAUTSAN - Arithmetic dynamics and residual periodicity of birational automorphisms of cubic surfaces |
|
We present "residual periodicity", a relatively new concept in arithmetic dynamics, as defined by Bandman, Grunewald and Kunyavskii. A rational self-map of a quasiprojective variety defined over a number field is strongly residually periodic if its minimal periods are bounded modulo almost every prime (where the bound is uniform, i.e. not depending on the prime). We discuss some interesting examples, and present results about residual periodicity of birational automorphisms of cubic surfaces.
|
How to come The journey to Enney is 2 hours from Geneva, 2h30 from Basel/Zurich, 1h30 from Lausanne. See timetables on www.cff.ch.
The train station of Enney is at 10 minutes by foot from the center. See the map, with the blue path given by google (pay attention to the snow!)
Participants
Ivan Bazhov (Geneva)
Mohammed Benzerga (Angers)
Cinzia Bisi (Ferrara)
Michel Brion (Grenoble)
Jérémy Blanc (Basel)
Serge Cantat (Rennes)
Jung Kyu Canci (Basel)
Adrien Dubouloz (Dijon)
Jean-Philippe Furter (La Rochelle)
Isac Héden (Uppsala)
Johannes Josi (Geneva)
Natalia Kolokolnikova (Geneva)
Nikon Kurnosov (Moscow)
Kevin Langlois (Grenoble)
Stéphane Lamy (Toulouse)
Matthias Leuenberger (Bern)
Lucy Moser-Jauslin (Dijon)
Frédéric Mangolte (Angers)
Charlie Petitjean (Dijon)
Pierre-Marie Poloni (Basel)
Yuri Prokhorov (Moscow)
Abdul Rauf (Bremen)
Andriy Regeta (Basel)
Maria Fernanda Robayo (Basel)
Christoph Schiessl (ETHZ)
Junliang Shen (ETHZ)
Mikhail Shkolnikov (Geneva)
Ronan Terpereau (Mainz)
Artur Tomberg (Moscow)
Christian Urech (Basel/Rennes)
Soli Vishkautsan (Ben-Gurion)
Susanna Zimmermann (Basel)
Send an email to Jeremy  Blanc  unibas  ch if you would like to participate.
Organisers
Adrien Dubouloz (Dijon)
Jérémy Blanc (Basel)
|
 unibas
unibas
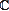 [x1,...,xn] )
[x1,...,xn] )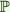
 . The group of birational diffeomorphisms of S is denoted by
. The group of birational diffeomorphisms of S is denoted by