|
Hamid AHMADINEZHAD - Singular quartic 3-folds and Sarkisov links |
| Quartic 3-folds with terminal singularities are among the simplest Fano varieties in three dimensions, yet their geometry is not well understood. In this talk I report on a work in progress, joint with Anne-Sophie Kaloghiros, which studies possible birational models of these objects. Sarkisov links via Cox rings of rank two are the natural method to tackle this problem. Some examples are explicitly described during the talk to illustrate this technique.
|
|
Emilie DUFRESNE - Invariants and Separating morphisms for algebraic group actions |
| We study the invariants of an algebraic group action on an affine variety via separating morphisms, that is, dominant G-invariant morphism to another affine variety such that points which are separated by some invariant have distinct image. This is a more geometric take on the study of separating invariants, a new trend in invariant theory initiated by Derksen and Kemper. In this talk, I will discuss some results which indicate that the fact that the invariants are not always finitely generated is less significant than the fact that what we would want to call the quotient morphism is not always surjective.
Joint work with Hanspeter Kraft.
|
|
Julien GRIVAUX - Deformations of rational surface automorphisms |
|
Although difficult to construct, rational surface automorphisms can occur in arbitrary large holomorphic families. In this talk, we will explain how the classical theory of deformations of complex manifolds of Kodaira and Spencer can be used to study deformations of rational surface automorphisms.
|
|
Stefan KEBEKUS - Singular spaces with trivial canonical class |
|
The classical Beauville-Bogomolov Decomposition Theorem
asserts that any compact Kähler manifold with numerically trivial
canonical bundle admits an étale cover that decomposes into a product
of a torus, and irreducible, simply-connected Calabi-Yau-- and
holomorphic-symplectic manifolds. The decomposition of the
simply-connected part corresponds to a decomposition of the tangent
bundle into a direct sum whose summands are integrable and stable with
respect to any polarisation.
Building on recent extension theorems for differential forms on
singular spaces, we prove an analogous decomposition theorem for the
tangent sheaf of projective varieties with canonical singularities and
numerically trivial canonical class. In view of recent progress in
minimal model theory, this result can be seen as a first step towards
a structure theory of manifolds with Kodaira dimension zero. Based on
our main result, we argue that the natural building blocks for any
structure theory are two classes of canonical varieties, which
generalise the notions of irreducible Calabi-Yau-- and irreducible
holomorphic-symplectic manifolds, respectively.
This is joint work with Daniel Greb and Thomas Peternell.
|
|
Hanspeter KRAFT - Varieties Characterized by their Endomorphims |
|
I will explain the following astonishing result: If two varieties X and Y have isomorphic endomorphism semigroups and if one of them is affine and contains a copy of the affine line, then X and Y are isomorphic up to base change.
The proof is based on some classical results of Dick Palais and uses tools from algebraic geometry and algebraic transformation groups.
Joint work with Rafael Andrist.
|
Stéphane LAMY - On the genus of birational selfmaps of 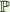 3, after Frumkin 3, after Frumkin |
|
В работе вводится понятие рода бирационального отображения неособых
трехмерных алгебраических многообразий над полем характеристики 0 и
доказывается, что автоморфизмы рода не больше фиксированного образуют
группу. В работе доказано, что бирациональный морфизм трехмерных
неособых многообразий разлагается в композицию отображения, обратного
морфизму рода 0, и моноидальных преобразований.
link
|
|
Kevin LANGLOIS -Affine T-varieties of complexity one
over an arbitrary field. |
| In this talk, we will explain that the presentation of an affine T-variety of complexity one in terms of polyhedral divisors holds over an arbitrary field.
|
|
Charlie PETITJEAN - A description of certain affine hyperbolic C*-varieties of complexity two. |
| The complexity of a T-variety X is defined to be the minimal codimension of the T-orbits in X. A variety toric is therefore a T-variety of complexity 0. Altmann and Hausen have given a more general description of T-affine varieties of any complexity, in terms of polyhedral divisors on quasi-projective varieties.
In this talk, I will review this construction for a class of affine threefolds of complexity 2 with a C*-action , with particular focus on the Koras-Russell threefolds and certain hyperbolic modifications.
|
 Conference in algebraic geometry - "Birpol3"
Conference in algebraic geometry - "Birpol3"