|
Rafael ANDRIST - Riemann surfaces in Stein manifolds with density property |
| Stein manifolds are the holomorphic analogue of affine manifolds. The density property ensures that the group of automorphisms is large enough to allow for many geometric constructions; this property holds e.g. for linear algebraic groups. The richness of the automorphism group can be exploited to construct proper holomorphic immersions/embeddings of non-compact Riemann surfaces into Stein manifolds with density property. As an application of this result, such manifolds can be characterized by their semigroup of endomorphisms.
|
|
Adrien DUBOULOZ - Automorphisms of A1-fibered surfaces |
| (Joint work with J. Blanc) A consequence of Jung's Theorem is that the automorphism group of the affine plane is generated by automorphisms that preserve suitable foliations by affine lines. It is a natural problem to decide if this property still holds for more general affine surfaces fibered by affine lines. In this talk, I briefly explain how a satisfactory answer to this question can be derived from a careful study of birational transformations between suitable projective models of these surfaces. I will give examples illustrating the various somehow unexpected properties of these automorphism groups.
|
|
Charles FAVRE - Isolated singularities admitting endomorphisms |
| We study complex algebraic isolated singularites admitting finite endomorphisms that are not automorphisms. We prove that these singularities are
log-canonical in a weak sense. An application of this result to the classification of
polarized endomorphisms is given. Joint work with Boucksom and De Fernex.
|
|
David FINSTON - Some elementary problems in non associative algebra and around the
cancellation problem |
|
For an algebraically closed field k and finite dimensional k-vector space
V,an m-ary algebra structure on V is a k-linear map μ : ⊗mV → V. The set of
m-ary algebra structures on V is identified with Akdm+1
in which the algebras with
no nontrivial ideals form a nonempty Zariski open subset. What is the structure of
the complement? Similarly, the algebras without nontrivial nilpotent elements form
a Zariski dense set and necessarily admit only finitely many automorphisms.
Does the automorphism group always have a nontrivial fixed subalgebra?
Winkelmann gave an example of a locally trivial Ga action on A5 with
strictly quasiaffine quotient W. A method is given to produce all affine total
spaces X of Ga bundles over W. Such X satisfy X × A1 A6; some X are
known to be isomorphic to A5, while the others remain undecided. Explicit
examples will be given of some of the undecided cases. The latter is joint
work with Adrien Dubouloz and Dilia Rueda, stemming from her thesis
research.
|
|
Hubert FLENNER - Infinite transitivity of automorphism groups of affine varieties |
| Given an affine algebraic variety X of dimension n ≥ 2, we let SAut(X) denote the
special automorphism group of X i.e., the subgroup of the full automorphism
group Aut(X) generated by all one-parameter unipotent subgroups. We
show that if SAut (X) is transitive on the smooth locus Xreg then it is
infinitely transitive on Xreg, i.e. n-transitive for every n ≥ 0. In turn, the
transitivity is equivalent to the flexibility of X. The latter means that for
every smooth point x ∈ Xreg the tangent space TxX is spanned by the
velocity vectors at x of one-parameter unipotent subgroups of Aut (X). We
provide also different variations and applications and connect our results to
former work of Forstneric and Rosay- Rudin in the complex analytic context.
|
|
Imad JARADAT - Proper Ga actions generated by monomial+1 derivations |
|
Every proper Ga action on A4 generated by a derivation δ of
ℂ[x1,x2,x3,x4] of the form:
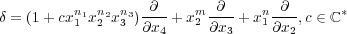
is conjugate to a translation with geometric quotient isomorphic to A3. A
derivation δ as above generates a proper action if and only if n1 > nn3 or
n2 ≡ m mod(m + 1).
|
|
Shulim KALIMAN - On the present state of the Andersen-Lempert theory |
| We present a survey of the Andersen-Lempert theory,
i.e. the study of the density property (which means that the Lie algebra
generated by completely integrable holomorphic vector fields on a given
Stein manifold
is dense in the space of all holomorphic vector fields). We discuss
also new results
one of which is the theorem stating that the product of Stein manifolds
with the volume density property (that is an analogue
of density property for fields of zero divergence)
possesses such a property as well.
|
|
Stéphane LAMY - Sarkisov links arising from the blow-up of a smooth space curve |
| I will present a joint work with Jérémy Blanc where we study smooth curves in P^3 whose blow-up produces a threefold with anticanonical divisor big and nef. In particular we are able to prove the existence of some Sarkisov links which were previously only known as numerical possibilities, and which correspond to elements in the Cremona group Bir(P^3) similar to the classical Geiser involution in dimension 2.
|
|
Ivan PAN - On generators for the de Jonquières group in dimension 3 |
| We consider birational maps J:P^n-->P^n which stabilize (birationally) the set of lines passing through a fixed point; the set of these maps constitutes a subgroup G of the Cremona group Cr_n of P^n. For n=2, generator sets for G and Cr_2 may be given by choosing a single element in G and a subgroup of linear automorphisms. In this talk we first note that for n=3 and d>1, every generator set for G (or Cr_3) contains uncountable many maps defined by polynomials of degree greater than d. Second we give an "interesting" set of generators for G; it is an open problem to know whether Cr_3 may be generated by elements in G and linear automorphisms.
|
|
Francesco RUSSO - Non associative algebras and Cremona transformations |
| I will report on joint work with Luc Pirio showing that every
quadro-quadric Cremona transformation of P^n is, modulo
projective transformation, the involution of a rank 3 complex
Jordan algebra.
If time allows we shall also outline that the previous
objects are in correspondence with very interesting
projective varieties.
|
|
Junyi XIE - Periodic points of birational maps of P^2 |
| We prove that the set of isolated periodic orbits of any birational map of P^2 with exponential growth of degrees is Zariski dense.
|
Conference on birational transformations and automorphisms of affine varieties
