|
|
5th Swiss-French workshop on algebraic geometry
Charmey (near Gruyères, Fribourg, Switzerland), January 18-22, 2016
The workshop was held in Charmey from January 18 to 22, 2016.
Mini-courses
In the morning, there will be three mini-courses of 5 hours (3 times one hour each day).
Ivan CHELTSOV (Edinburgh)
|
G-birationally rigid rational Fano threefolds |
|
|
|
|
Robin DE JONG (Leiden) |
Intersection theory on arithmetic surfaces |
|
|
|
Jean FASEL (Grenoble)
|
Unstable classification of vector bundles over smooth affine schemes |
|
|
|
In the afternoon, we will have research talks of 50 minutes.
Schedule Talks: In Charmey, ( "Centre Les Dents Vertes, Viva-Gruyère" )
Monday
January 18
|
Tuesday
January 19
|
Wednesday
January 20 |
Thursday
January 21 |
Friday
January 22 |
12h30 welcome
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
breakfast
8h45-9h45
mini-course 1
10h15-11h15
mini-course 2
11h45-12h45
mini-course 3
|
breakfast
8h45-9h45
mini-course 1
10h-11h
mini-course 2
11h15-12h15
mini-course 3
|
| lunch |
lunch |
lunch |
lunch |
|
14h30-15h30
mini-course 1
16h00-17h00
mini-course 2
17h30-18h30
mini-course 3
dinner
|
time for discussion / enjoying the mountain
17h20-18h10
L. Frey
18h30-19h20
T. Pełka
dinner
|
time for discussion / enjoying the mountain
17h20-18h10
L. Kühne
18h30-19h20
N. Kalinin
dinner
|
time for discussion / enjoying the mountain
16h10-17h00
F. Veneziano
17h20-18h10
I. Krylov
18h30-19h20
R. Terpereau
dinner
|
|
Mini-courses - titles and abstracts
|
Ivan CHELTSOV -
G-birationally rigid rational Fano threefolds |
|
For a rational Fano threefold X faithfully acted by a finite group G, being G-birationally rigid means
that X is the unique output of a G-equivariant Minimal Model Program, i.e. X is a G-Mori fiber space over a point,
and X is not G-birational to any other G-Mori fiber space.
We describe existing methods of proving G-birational rigidity of Fano threefolds,
and apply them to construct many explicit examples of rational G-birationally rigid Fano threefolds.
As an application we obtain many examples of non-conjugate embeddings of finite groups into the Cremona group of rank 3.
|
|
Robin DE JONG - Intersection theory on arithmetic surfaces |
|
Arithmetic surfaces are certain 2-dimensional models of curves defined over a number field. One can develop an intersection theory on arithmetic surfaces in analogy with the classical intersection theory on projective surfaces over a field, involving such results as adjunction formula, Riemann-Roch and a Noether formula. Arithmetic intersection numbers involve both non-archimedean data (coming from the finite primes of the number field) and archimedean data (coming from the embeddings of the number field into the complex numbers). These archimedean data are given by complex analytic Green's functions, which make arithmetic intersection numbers both hard to compute and interesting to study. Recently it has become clear that these Green's functions, when studied in degenerating families of compact Riemann surfaces, themselves display a certain asymptotic behavior whose leading terms can be explained by the non-archimedean data in arithmetic intersection theory.
|
|
Jean FASEL - Unstable classification of vector bundles over smooth affine schemes |
|
In these lectures, we will explain how to classify vector bundles on smooth affine schemes using the machinery of the A^1-homotopy category. We will start with a quick introduction on the A^1-homotopy category, and then explain the results of Morel on the classification of vector bundles. We will then explain how to extend these results using Postnikov towers, together with the known computations of the second non trivial A^1-homotopy sheaf of the affine punctured space of a given dimension. Time permitting, we wil also explain how to classify symplectic or orthogonal bundles.
|
Talks - titles and abstracts
|
Linda FREY - Heights and elliptic curves |
|
After shortly introducing heights and elliptic curves we will look at the torsion points Etor of an elliptic curve E over 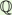 and adjoin their coordinates to and adjoin their coordinates to 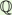 . What we get is . What we get is 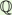 (Etor) which is a Bogomolov field. In a Bogomolov field, the height of a nonzero number which is not a root of unity is bounded from below by a positive constant. We will compute this constant explicitly and give an overview of the proof. (Etor) which is a Bogomolov field. In a Bogomolov field, the height of a nonzero number which is not a root of unity is bounded from below by a positive constant. We will compute this constant explicitly and give an overview of the proof.
|
|
Nikita KALININ -
Tropical curves and sandpile models |
|
We will discuss sandpile models. They concern moving chips on the vertices of some graph and emerge in many different places: physics, combinatorics, and algebraic geometry. In a particular situation, when we perturb the maximal stable state by adding a few chips, we will see emergence of tropical curves, aka planar graphs with straight edges with rational slopes, and balancing condition at vertices. If time permits, we will discuss the initial motivation for defining such models as well as speculations about the future development.
|
|
Lars KÜHNE - A glimpse of anabelian geometry |
|
|
|
Igor KRYLOV - Classification and birational rigidity of del Pezzo fibrations with an action of the Klein simple group |
|
Study of embeddings of a finite group G into the Cremona group is equivalent to study of G-birational geometry of rational G-Mori fiber spaces. A good place to start study finite subgroups is a study of simple subgroup. We prove that any del Pezzo fibration over projective line with an action of the Klein simple group is either a direct product or a certain singular del Pezzo fibration Xn of degree 2. It is known that del Pezzo fibrations of degree 2 satisfying the K^2-condition are birationally superrigid. I extend this result to singular del Pezzo fibrations and prove that Xn are superrigid, in particular not rational, for n>2.
|
TOMASZ PEŁKA - Planar cuspidal curves with 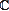 **-fibered complements **-fibered complements |
|
To classify complex rational cuspidal curves E⊂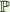 2 it remains to classify these whose complements are of log general type, i.e. these for which κ(KX+D)=2, where (X,D) is a log resolution of ( 2 it remains to classify these whose complements are of log general type, i.e. these for which κ(KX+D)=2, where (X,D) is a log resolution of (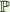 2,E). It is conjectured that κ(KX+1/2D)=-&infty; and hence 2,E). It is conjectured that κ(KX+1/2D)=-&infty; and hence 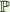 2\E is 2\E is 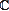 **-fibered, where **-fibered, where 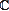 **= **=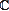 \{0,1}, or -(KX+\frac{1}{2}D) is ample on some minimal model of (X,1/2D). A vast majority of known examples turns out to be of the first type. We discuss our recent progress on their classification. This is a joint project with Karol Palka. \{0,1}, or -(KX+\frac{1}{2}D) is ample on some minimal model of (X,1/2D). A vast majority of known examples turns out to be of the first type. We discuss our recent progress on their classification. This is a joint project with Karol Palka.
|
|
Ronan TERPEREAU - Maximal connected subgroups of the Cremona groupk |
|
This talk is about a work in progress with Jérémy Blanc and Andrea Fanelli. The so-called Cremona group is the group of birational transformations of the n-dimensional complex projective space. This group is not an algebraic group for n>1, but we can hope (at least in small dimension) classify its maximal connected algebraic subgroups. In dimension 2, the classification is old and quite easy (F. Enriques, 1893). In dimension 3, the first rigorous treatment was done by H. Umemura in the 1980's in a series of six (quite long and technical) papers. In this talk I will explain how we can hope to recover his results in a much simpler way using the now well-developed Mori theory and discuss several possible generalizations.
|
|
Francesco VENEZIANO - Rational points on explicit families of curves
|
|
I will present a method, of easy application, to compute all the
rational points on a fairly general family of curves in products of elliptic
curves, proving in particular the explicit Mordell-Lang Conjecture for
these curves. We prove some explicit and very sharp estimates for the height
of such rational points. The bounds are so good that we can implement a
computer search. I will present several explicit examples in which this has
been done.
All results are in collaboration with Sara Checcoli and Evelina Viada.
|
How to come
The address is VIVA GRUYERE Charmey Rte des Arses 4 1637 Charmey
The journey to Charmey is 2h10 from Geneva, 2h30 from Basel/Zurich, 1h30 from Lausanne. See timetables on www.cff.ch, the bus stop is "Charmey (Gruyère), Le Chêne". The place is very near the bus stop. See the map
Participants
Raphaël Achet (Grenoble)
Rémi Bignalet-Cazalet (Dijon)
Cinzia Bisi (Ferrara)
Jérémy Blanc (Basel)
Jung-Kyu Canci (Basel)
Ivan Cheltsov (Edinburgh)
Robin De Jong (Leiden)
Adrien Dubouloz (Dijon)
Andrea Fanelli (Basel)
Jean Fasel (Grenoble)
Linda Frey (Basel)
Jean-Philippe Furter (Basel)
Philipp Habegger (Basel)
Isac Hedén (Kyoto)
Mattias Hemmig (Basel)
Johannes Josi (Genève)
Nikita Kalinin (Genève)
Lars Kühne (Bonn)
Igor Krylov (Edinburgh)
Stéphane Lamy (Toulouse)
Bruno Laurent (Grenoble)
Anne Lonjou (Toulouse)
Lucy Moser-Jauslin (Dijon)
Jan Nagel (Dijon)
Karol Palka (Warsaw)
Tomasz Pełka (Warsaw)
Pierre-Marie Poloni (Bern)
Lukas Pottmeyer (Basel)
Maria Fernanda Robayo (Basel)
Andriy Regeta (Basel)
Immanuel Stampfli (Hamburg)
Stefan Schmid (Basel)
Ronan Terpereau (Bonn)
Christian Urech (Basel/Rennes)
Francesco Veneziano (Basel)
Susanna Zimmermann (Basel)
Send an email to Jeremy  Blanc  unibas  ch if you would like to participate.
Organisers
Adrien Dubouloz (Dijon)
Philipp Habegger (Basel)
Jérémy Blanc (Basel)
|
 unibas
unibas and adjoin their coordinates to
and adjoin their coordinates to